题目内容
如图,在△ABC 中,∠C=90°,AC=2,点 D 在 BC 上,∠ADC=2∠B,AD=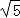 ,则 BC 的长为
,则 BC 的长为
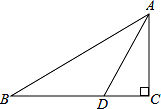 ( )
( )
A.  ﹣1 B.
﹣1 B.  +1 C.
+1 C. 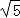 ﹣1 D.
﹣1 D. 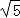 +1
+1
D【考点】勾股定理;等腰三角形的判定与性质.
【专题】压轴题.
【分析】根据∠ADC=2∠B,∠ADC=∠B+∠BAD 判断出 DB=DA,根据勾股定理求出 DC 的长,从 而求出 BC 的长.
【解答】解:∵∠ADC=2∠B,∠ADC=∠B+∠BAD,
D∴∠B=∠DAB,
∴DB=DA= 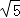 ,
,
在 Rt△ADC 中,
DC= 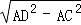 =
= 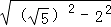 =1;
=1;
∴BC= 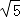 +1.
+1.
故选 D.
【点评】本题主要考查了勾股定理,同时涉及三角形外角的性质,二者结合,是一道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )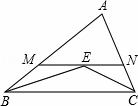
 个除颜色外完全相同的球,这
个除颜色外完全相同的球,这 3个.若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱.通过大量重复摸球试验后发现,摸到红球的频率稳定在20%附近,那么可以推算出
3个.若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱.通过大量重复摸球试验后发现,摸到红球的频率稳定在20%附近,那么可以推算出
 经过两次下调后,决定以每平方米4860元的均价开盘销售.
经过两次下调后,决定以每平方米4860元的均价开盘销售.