题目内容
 已知直线BC:y=-2x-4与x轴交于B点,与y轴交于C点,A点的坐标为(-4,-1),连接AC、AB
已知直线BC:y=-2x-4与x轴交于B点,与y轴交于C点,A点的坐标为(-4,-1),连接AC、AB(1)判断△ABC的形状;
(2)如果将△ABC沿着AB旋转一周,求所得的旋转体的体积.
分析:(1)由直线BC:y=-2x-4与x轴交于B点,与y轴交于C点,可求得点B与C的坐标,又由A点的坐标为(-4,-1),利用两点式,即可求得AB,AC,BC的长,然后由勾股定理的逆定理,即可判定△ABC的形状;
(2)由△ABC沿着AB旋转一周,可得圆锥,且圆锥的底面是以BC为半径的圆,圆锥的高是AB,然后利用圆锥的体积公式求解即可求得答案.
(2)由△ABC沿着AB旋转一周,可得圆锥,且圆锥的底面是以BC为半径的圆,圆锥的高是AB,然后利用圆锥的体积公式求解即可求得答案.
解答:解:(1)∵直线BC:y=-2x-4与x轴交于B点,与y轴交于C点,
∴B(-2,0),C(0,-4),
∵A点的坐标为(-4,-1),
∴AB2=[-4-(-2)]2+(-1-0)2=5,AC2=(-4-0)2+[(-1-(-4)]2=25,BC2=22+42=20,
∴AB=
,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,且∠ABC=90°;
(2)∵△ABC沿着AB旋转一周,可得圆锥,且圆锥的底面是以BC为半径的圆,圆锥的高是AB,
∴所得的旋转体的体积为:
×π×BC2×AB=
×π×20×
=
π.
∴B(-2,0),C(0,-4),
∵A点的坐标为(-4,-1),
∴AB2=[-4-(-2)]2+(-1-0)2=5,AC2=(-4-0)2+[(-1-(-4)]2=25,BC2=22+42=20,
∴AB=
| 5 |
∴AB2+BC2=AC2,
∴△ABC是直角三角形,且∠ABC=90°;
(2)∵△ABC沿着AB旋转一周,可得圆锥,且圆锥的底面是以BC为半径的圆,圆锥的高是AB,
∴所得的旋转体的体积为:
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
20
| ||
| 3 |
点评:此题考查了一次函数的性质、勾股定理的逆定理以及圆锥的体积公式.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目

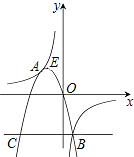 (2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线
(2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线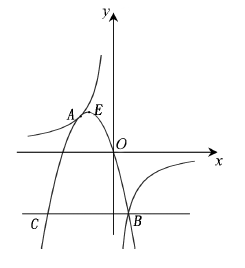
 相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.