题目内容
2.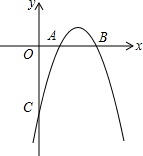 如图,抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
如图,抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).(1)则抛物线的解析式是y=-x2+4x-3顶点坐标是(2,1);
(2)平移抛物线,使平移后抛物线的顶点落在直线y=-x上,且过原点O,求平移后抛物线的解析式;
(3)若原抛物线的顶点在射线y=0.5x(x>0)上滑动,且过点(0,-14),应该怎样平移原抛物线?
分析 (1)根据待定系数法列出方程组即可解决问题,再利用配方法求出顶点坐标即可.
(2)设平移后的抛物线顶点为(m,0.5m),则抛物线为y=-(x-m)2+0.5m,把(0,-14)代入求出m的值即可解决问题.
解答 解:(1)由题意得$\left\{\begin{array}{l}{a+b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\\{c=-3}\end{array}\right.$,
故抛物线解析式为y=-x2+4x-3=-(x-2)2+1,
故顶点坐标(2,1).
故答案为y=-x2+4x-3,(2,1).
(2)由题意顶点(0,0),抛物线解析式为y=-x2.
(3)设平移后的抛物线顶点为(m,0.5m),则抛物线为y=-(x-m)2+0.5m,
把(0,-14)代入得到2m2-m-28=0,解得m=4或-$\frac{7}{2}$,
m=4时抛物线为y=-(x-4)2+2,顶点为(4,2),
m=-$\frac{7}{2}$时,抛物线为y=-(x+$\frac{7}{2}$)2-$\frac{7}{4}$,顶点为(-$\frac{7}{2}$,-$\frac{7}{4}$).
故原抛物线向右平移2个单位再向上平移1个单位得到,或原抛物线向左平移$\frac{11}{2}$个单位再向下平移$\frac{11}{4}$个单位得到.
点评 本题考查抛物线与x轴的交点、平移问题、一次函数等知识,解题的关键是熟练掌握二次函数的有关性质,学会设参数解决问题,记住平移坐标的变化规律,属于中考常考题型.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | x•2x=2x | B. | x3•x2=x5 | C. | (x2)3=x5 | D. | (2x)2=2x2 |
10.有下列长度的三条线段,能组成三角形的是( )
| A. | 3cm,4cm,8cm | B. | 4cm,4cm,8cm | C. | 5cm,6cm,10cm | D. | 2cm,5cm,10cm |
7.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是70cm和48cm,则△ABC的腰和底边长分别为( )
| A. | 24cm和22cm | B. | 26cm和18cm | C. | 22cm和26cm | D. | 23cm和24cm |
14.点P(a,2)在第一象限,则点Q(-2,a+1)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
 如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( ) 如图,△ABC是△DEF向右平移4个单位长度后得到的,且三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC是△DEF向右平移4个单位长度后得到的,且三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).