题目内容
如图所示，点P，Q，C都在直线AB上，且P是AC的中点，Q是BC的中点，若AC=m，BC=n，则线段PQ的长为
- A.
- B.
- C.
- D.
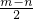
C
分析：根据题意，结合图形，可求得PC=
AC、CQ=BC，故PQ=PC+CQ可求．
解答：∵P是AC的中点
∴PC=AC
∵Q是BC的中点
∴CQ=BC
若AC=m，BC=n
则PQ=PC+CQ=AC+BC
=
故选C．
点评：利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．
分析：根据题意，结合图形，可求得PC=
AC、CQ=BC，故PQ=PC+CQ可求．解答：∵P是AC的中点
∴PC=
AC∵Q是BC的中点
∴CQ=
BC若AC=m，BC=n
则PQ=PC+CQ=
AC+BC=
故选C．
点评：利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．
练习册系列答案
阅读快车系列答案
相关题目
11、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，正方形ABCD的边长为4，FG=3，FP=1，则△DEK的面积为
8、正方形ABCD，正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，且G为BC的三等分点，R为EF中点，正方形BEFG的边长为4，则△DEK的面积为（ ）
（2012•鄂州）在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第2012个正方形的面积为（ ）
如图所示，点C在线段BE上，在BE同侧作等边△ABC和等边△DCE，那么，从旋转的角度我们可以看到，△ACE旋转后与△BCD重合．