题目内容
如图，D为等边△ABC边AC的中点，E是BC延长线上一点，且CE=
BC，则△DBE是一个________三角形．（只填出一个你认为正确的结论．）
等腰三角形
分析：由题意可知∠DBC=30°，∠ACB=60°，由CE=BC，推出DC=CE，所以∠E=∠CDE=30°，即可知△DBE是一个等腰三角形．
解答：∵D为等边△ABC边AC的中点，
∴∠DBC=30°，∠ACB=60°，
∵CE=BC，
∴DC=CE，
∵∠ACB=∠E+∠CDE，
∴∠E=∠CDE=30°，
∴△DBE是一个等腰三角形．
故答案为等腰三角形．
点评：本题主要考查等边三角形的性质、等腰三角形的判定，关键在于求出∠E的度数．
分析：由题意可知∠DBC=30°，∠ACB=60°，由CE=
BC，推出DC=CE，所以∠E=∠CDE=30°，即可知△DBE是一个等腰三角形．解答：∵D为等边△ABC边AC的中点，
∴∠DBC=30°，∠ACB=60°，
∵CE=
BC，∴DC=CE，
∵∠ACB=∠E+∠CDE，
∴∠E=∠CDE=30°，
∴△DBE是一个等腰三角形．
故答案为等腰三角形．
点评：本题主要考查等边三角形的性质、等腰三角形的判定，关键在于求出∠E的度数．
练习册系列答案
相关题目
3、如图，△ABC为等边三角形，∠ABC、∠ACB的平分线相交于点O，OE∥AB交BC于点E，OF∥AC交BC于点F，图中等腰三角形共有（ ）
如图，△ABC为等边三角形，点D，E，F分别在AB，BC，CA边上，且△DEF是等边三角形，求证：△ADF≌△CFE．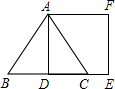
如图，△ABC为等边三角形，AD为BC边上的高，且AB=2，则正方形ADEF的面积为
（2013•普陀区模拟）如图，△AOB为等边三角形，点B的坐标为（-2，0），过点C（2，0）作直线l交AO于点D，交AB于E，点E在反比例函数
如图，△AOB为等边三角形，点B的坐标为（-2，0），过点C（2，0）作直线l交AO于D，交AB于E，点E在某反比例函数图象上，当△ADE和△DCO的面积相等时，那么该反比例函数解析式为（ ）