题目内容
如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针方向旋转60°到OD,则PD的长为( )
A.

B.

C.

D.2

【答案】分析:作DE⊥CB于E,根据题意先求得∠AOP=60°,∠DOC=60°.利用三角函数可求DE= ,EO=
,EO= .根据勾股定理即可求PD的值.
.根据勾股定理即可求PD的值.
解答: 解:如图,作DE⊥CB于E.
解:如图,作DE⊥CB于E.
∵OB=PB=1,
∴OA=1.
又∵PA切⊙O于点A,
则OA⊥AP,
∴∠AOP=60°.
又∵OA绕点O逆时针方向旋转60°,
∴∠DOC=60°.
∴DE=1×sin60°= ,EO=
,EO= .
.
∴PD= =
= .
.
故选A.
点评:考查了勾股定理和解直角三角形的知识及切线的性质.
 ,EO=
,EO= .根据勾股定理即可求PD的值.
.根据勾股定理即可求PD的值.解答:
 解:如图,作DE⊥CB于E.
解:如图,作DE⊥CB于E.∵OB=PB=1,
∴OA=1.
又∵PA切⊙O于点A,
则OA⊥AP,
∴∠AOP=60°.
又∵OA绕点O逆时针方向旋转60°,
∴∠DOC=60°.
∴DE=1×sin60°=
 ,EO=
,EO= .
.∴PD=
 =
= .
.故选A.
点评:考查了勾股定理和解直角三角形的知识及切线的性质.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
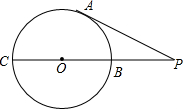 如图,PA切⊙O于点A,PC过点O且于点B、C,若PA=6cm,PB=4cm,则⊙O的半径为
如图,PA切⊙O于点A,PC过点O且于点B、C,若PA=6cm,PB=4cm,则⊙O的半径为 21、如图,PA切⊙O于点A,割线PBC交⊙O于B、C两点,∠APC的平分线分别交AC、AB于D、E两点.请在图中找出2对相似三角形,并从中选择一对相似三角形说明其为什么相似.
21、如图,PA切⊙O于点A,割线PBC交⊙O于B、C两点,∠APC的平分线分别交AC、AB于D、E两点.请在图中找出2对相似三角形,并从中选择一对相似三角形说明其为什么相似. 6、如图,PA切⊙O于点A,PBC是经过O点的割线,若∠P=30°,则弧AB的度数是( )
6、如图,PA切⊙O于点A,PBC是经过O点的割线,若∠P=30°,则弧AB的度数是( )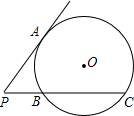 如图,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA=
如图,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA= 如图,PA切⊙O于点A,PBC是经过圆心的割线,并与圆相交于点B,C.若PC=9,PA=3,则∠P的余弦值是( )
如图,PA切⊙O于点A,PBC是经过圆心的割线,并与圆相交于点B,C.若PC=9,PA=3,则∠P的余弦值是( )