题目内容
（1）（-3a）3-（-a）•（-3a）2；
（2）（n-m）3•（m-n）2-（m-n）5；
（3）（-22）3+22×24+（
）0+|-5|-（
）-1；
（4）0.125 2004×（-8）2005．
（2）（n-m）3•（m-n）2-（m-n）5；
（3）（-22）3+22×24+（
| 1 |
| 125 |
| 1 |
| 7 |
（4）0.125 2004×（-8）2005．
考点：整式的混合运算
专题：计算题
分析：（1）原式利用积的乘方及幂的乘方运算法则计算，合并即可得到结果；
（2）原式第一项变形后利用同底数幂的乘法法则计算，合并即可得到结果；
（3）原式第一项利用幂的乘方及积的乘方运算法则计算，第二项利用同底数幂的乘法法则计算，第三项利用零指数幂法则计算，第四项利用绝对值的代数意义化简，最后一项利用负指数幂法则计算即可得到结果；
（4）原式变形后逆用积的乘方运算法则计算，即可得到结果．
（2）原式第一项变形后利用同底数幂的乘法法则计算，合并即可得到结果；
（3）原式第一项利用幂的乘方及积的乘方运算法则计算，第二项利用同底数幂的乘法法则计算，第三项利用零指数幂法则计算，第四项利用绝对值的代数意义化简，最后一项利用负指数幂法则计算即可得到结果；
（4）原式变形后逆用积的乘方运算法则计算，即可得到结果．
解答：解：（1）原式=-27a3+9a3=-18a3；
（2）原式=-（m-n）5-（m-n）5=-2（m-n）5；
（3）原式=-64+64+1+5-7=-1；
（4）原式=（-0.125×8）2004×（-8）=-8．
（2）原式=-（m-n）5-（m-n）5=-2（m-n）5；
（3）原式=-64+64+1+5-7=-1；
（4）原式=（-0.125×8）2004×（-8）=-8．
点评：此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
小题狂做系列答案
相关题目
使代数式
有意义的x的取值范围是（ ）
| ||
| 2x-6 |
| A、x≠3 |
| B、x＜5且x≠3 |
| C、x≤5且x≠2 |
| D、x≤5且x≠3 |
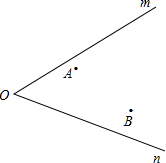电信部门要建一座发射塔，如图：按照设计要求，发射塔建在高速公路m和n所夹右侧区域且到城镇A、B距离相等，到两条高速公路m和n的距离也必须相等，发射塔应建在什么位置？请标出它的位置．（保留作图痕迹）
如图，已知AB是⊙O的直径，BC⊥AB，连结OC，弦AD∥OC，直线CD交BA的延长线于点E．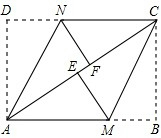
已知：如图，在矩形ABCD中，把∠B、∠D分别翻折，使点B、D分别落在对角线AC上的点E、F处，折痕分别为AN、CM．