题目内容
 数学兴趣小组活动课上测量电线杠的高度,在位于电线杆两侧的A、B处(点A、B及电线杆底部F在同一直线上)测得电线杆顶部E的仰角分别为45°和36°(如图).已知测量仪器距离地面都是1.5m,两测点A、B的距离是20m.求电线杆EF的高度(tan54°=1.38,结果精确到0.1m).
数学兴趣小组活动课上测量电线杠的高度,在位于电线杆两侧的A、B处(点A、B及电线杆底部F在同一直线上)测得电线杆顶部E的仰角分别为45°和36°(如图).已知测量仪器距离地面都是1.5m,两测点A、B的距离是20m.求电线杆EF的高度(tan54°=1.38,结果精确到0.1m).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:连接CD交EF于点H,可得CD⊥EF,设EH=x,在Rt△CEH和Rt△DEH中,分别表示出CH和DH的长度,根据CD=AB=20米,列方程求出x的值,继而可求得EF的长度.
解答:解:连接CD交EF于点H,可得CD⊥EF,
设EH=x,
在Rt△CEH中,∠ECH=45°,
∴∠CEH=45°,
∴CH=EH=x,
在Rt△DEH中,
∠EDH=36°,tan∠DEH=
,
∠DEH=90°-36°=54°,
∴tan54°=
,
∴HD=tan54°x,
∵CH+DH=AB=20,
∴x+tan54°x=20,
解得:x≈8.40,
∴EF=EH+HF≈8.40+1.5=9.9(m),
即电线杆高为9.9m.
设EH=x,

在Rt△CEH中,∠ECH=45°,
∴∠CEH=45°,
∴CH=EH=x,
在Rt△DEH中,
∠EDH=36°,tan∠DEH=
| HD |
| EH |
∠DEH=90°-36°=54°,
∴tan54°=
| HD |
| EH |
∴HD=tan54°x,
∵CH+DH=AB=20,
∴x+tan54°x=20,
解得:x≈8.40,
∴EF=EH+HF≈8.40+1.5=9.9(m),
即电线杆高为9.9m.
点评:本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
相关题目
截止2013年10月余额宝规模达到2 175000 000元,用科学记数法表示捐款数应为( )
| A、2.175×1010元 |
| B、2.175×109元 |
| C、21.75×108元 |
| D、217.5×107元 |
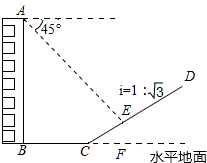 如图,一楼房AB后有一假山,其坡度为i=1:
如图,一楼房AB后有一假山,其坡度为i=1: