题目内容
如图10，AB∥FC，D是AB上一点，DF交AC于点E，DE=FE，分别延长FD和CB交于点G.
(1) 求证：△ADE≌△CFE；
(2) 若GB=2，BC=4，BD=1，求AB的长.
图10
 |
(1) ∵ AB∥FC，∴∠ADE=∠CFE
又∵∠AED=∠CEF，DE=FE
∴ △ADE≌△CFE（ASA）
(2) ∵ △ADE≌△CFE，∴ AD=CF
∵ AB∥FC，∴∠GBD＝∠GCF，∠GDB＝∠GFC
∴ △ GBD∽△GCF（AA）
∴ 
又因为GB＝2，BC＝4，BD＝1，代入得：CF＝3 = AD
∴ AB＝AD+BD = 3+1 = 4
练习册系列答案
相关题目
A. B.
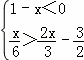，并把它的解集在数轴上表示出来．
ABCD 中，点E是AD的中点，延长BC到点F，使CF : BC=1 : 2，连接DF，EC.若AB=5，AD=8，sinB=
，则DF的长等于 ( )
（B）
（C）
（D）
ABC是等腰直角三角形，AC=BC=
，以斜边AB上的点O为圆心的圆分别与AC，BC相切与点E，F， 与AB 分别交于点G，H，且 EH 的延长线和 CB 的延长线交于点D，则 CD 的长为 .
