题目内容
7.一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$,那么铅球运动过程中最高点离地面的距离为3米.分析 直接利用配方法求出二次函数最值即可.
解答 解:由题意可得:
y=-$\frac{1}{12}{x^2}+\frac{2}{3}x+\frac{5}{3}$
=-$\frac{1}{12}$(x2-8x)+$\frac{5}{3}$
=-$\frac{1}{12}$(x-4)2+3,
故铅球运动过程中最高点离地面的距离为:3m.
故答案为:3.
点评 此题主要考查了二次函数的应用,正确利用配方法求出最值是解题关键.

练习册系列答案
相关题目
18.已知⊙O是以坐标原点O为圆心,5为半径的圆,点M的坐标为(-3,4),则点M与⊙O的位置关系为( )
| A. | M在⊙O上 | B. | M在⊙O内 | C. | M在⊙O外 | D. | M在⊙O右上方 |
2.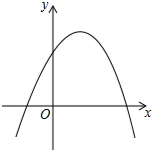 如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
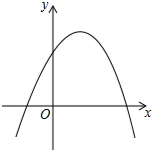 如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )| A. | a<0,b>0,c>0 | B. | a>0,b<0,c>0 | C. | a>0,b>0,c<0 | D. | a<0,b<0,c<0 |
20.已知下列算式:①|-3|=3;②-32=6;③(-1)2016=1;④2xy-xy=xy.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
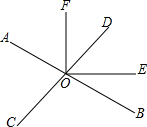 如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.
如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.