题目内容
 如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)△AEC≌△ABF;
(2)EC⊥BF.
分析:(1)求出∠EAC=∠BAF,根据SAS推出两三角形全等即可.
(2)根据全等得出∠ACE=∠AFB,求出∠AFB+∠AOF=90°,推出∠ACE+∠COM=90°,求出∠CMF=180°-90°=90°即可.
(2)根据全等得出∠ACE=∠AFB,求出∠AFB+∠AOF=90°,推出∠ACE+∠COM=90°,求出∠CMF=180°-90°=90°即可.
解答:证明:(1)∵AE⊥AB,AF⊥AC,
∴∠EAB=∠FAC=90°,
∴∠EAB+∠BAC=∠FAC+∠BAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中
∴△AEC≌△ABF(SAS).
(2)∵△AEC≌△ABF,
∴∠ACE=∠AFB,
∵∠FAC=90°,
∴∠AFB+∠AOF=90°,
∴∠ACE+∠AOF=90°,
∵∠AOF=∠COM,
∴∠ACE+∠COM=90°,
∴∠CMF=180°-90°=90°,
∴EC⊥BF.
∴∠EAB=∠FAC=90°,
∴∠EAB+∠BAC=∠FAC+∠BAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中
|
∴△AEC≌△ABF(SAS).
(2)∵△AEC≌△ABF,

∴∠ACE=∠AFB,
∵∠FAC=90°,
∴∠AFB+∠AOF=90°,
∴∠ACE+∠AOF=90°,
∵∠AOF=∠COM,
∴∠ACE+∠COM=90°,
∴∠CMF=180°-90°=90°,
∴EC⊥BF.
点评:本题考查了三角形的内角和定理,全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
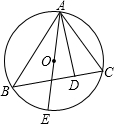 如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.
如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.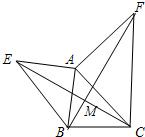
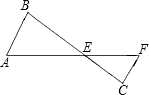 如图所示,已知AE=54,BE=45,FE=36,CE=30,CF=26.
如图所示,已知AE=54,BE=45,FE=36,CE=30,CF=26.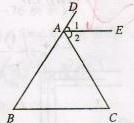 24、如图所示,已知AE∥BC,∠B=∠C.
24、如图所示,已知AE∥BC,∠B=∠C.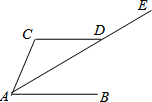 (2013•宜春模拟)如图所示,已知AE平分∠BAC交CD于点D,且AB∥CD,∠C=100°,则∠EAC为( )
(2013•宜春模拟)如图所示,已知AE平分∠BAC交CD于点D,且AB∥CD,∠C=100°,则∠EAC为( )