题目内容
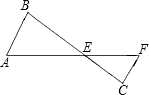如图所示，已知AE=54，BE=45，FE=36，CE=30，CF=26．（1）请证明：△AEB∽△FEC．
（2）试求AB的长．
分析：（1）根据已知可求得AE：EF=BE：CE，已知∠AEB=∠FEC，从而根据两组边对应成比例且其夹角相等的两个三角形相似求证即可．
（2）根据相似三角形的对应边成比例不难求得AB的长．
（2）根据相似三角形的对应边成比例不难求得AB的长．
解答：证明：（1）∵
=
=
（1分）
=
=
（2分）
∴
=
（3分）
又∵∠AEB=∠FEC（4分）
∴△AEB∽△FEC；（5分）
解：（2）∵△AEB∽△FEC
∴
=
（6分）
∵AE=54，BE=45，FE=36，CE=30，CF=26
∴
=
（7分）
∴AB=39
即AB的长为39．（8分）
| AE |
| FE |
| 54 |
| 36 |
| 3 |
| 2 |
| BE |
| CE |
| 45 |
| 30 |
| 3 |
| 2 |
∴
| AE |
| FE |
| BE |
| CE |
又∵∠AEB=∠FEC（4分）
∴△AEB∽△FEC；（5分）
解：（2）∵△AEB∽△FEC
∴
| AB |
| CF |
| AE |
| FE |
∵AE=54，BE=45，FE=36，CE=30，CF=26
∴
| AB |
| 26 |
| 54 |
| 36 |
∴AB=39
即AB的长为39．（8分）
点评：此题主要考查学生对相似三角形的判定及性质的理解及运用能力．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
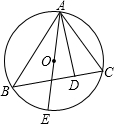如图所示，已知AE为⊙O的直径，AD为△ABC的BC边上的高．
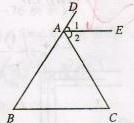24、如图所示，已知AE∥BC，∠B=∠C．
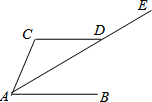（2013•宜春模拟）如图所示，已知AE平分∠BAC交CD于点D，且AB∥CD，∠C=100°，则∠EAC为（ ）