题目内容
已知点A(-2,n)在抛物线y=x2+bx+c上.
(1)若b=1,c=3,求n的值;
(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点
P(x-1,x2+bx+c)的纵坐标随横坐标 变化的图象,并说明理由.
变化的图象,并说明理由.
(1)解:∵ b=1,c=3,
∴ y=x2+x+3.
∵点A(-2,n)在抛物线y=x2+x+3上,
∴n=4-2+3
=5.
(2)解:∵点A(-2,n),B(4,n)在抛物线y=x2+bx+c上,
∴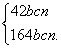 ∴b=-2.
∴b=-2.
∴顶点的横坐标是-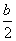 =1.
=1.
即顶点为(1,-4).
∴-4=1-2+c.
∴c=-3.
∴P(x-1,x2-2x-3).
∵将点(x,x2-2x-3)向左平移一个单位得点P(x-1,x2-2x-3),
∴将点(x,x2-2x-3)的纵坐标随横坐标变化的函数的图象向左平移
一个单位后可得点P(x-1,x2-2x-3)的纵坐标随横坐标变化的函
数的图象.
设p=x-1,q=x2-2x-3,
则q=p2-4.
画出抛物线q=p2-4的图象.

练习册系列答案
相关题目

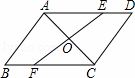
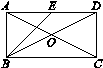
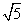 ,则BO= ,∠EBD的大小约为
,则BO= ,∠EBD的大小约为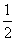 )
)

 摸取1个,摸到红球的概率是( )
摸取1个,摸到红球的概率是( ) B.
B.  C.
C.  D.
D. 
 )÷
)÷ ,其中x=(π﹣2015)0﹣
,其中x=(π﹣2015)0﹣ +(
+( )﹣1.
)﹣1.