题目内容
已知直角三角形ABC中，∠C=90°，AC=6，BC=8，现将△ABC绕点B旋转90°，得△DBE，其中A的对应点为E，则AE的长为（ ）
| A、20 | ||
B、10
| ||
C、20
| ||
| D、10 |
分析：根据勾股定理可得出AB=10，根据将△ABC绕点B旋转90°，得出的△DBE为直角三角形，再根据勾股定理即可得出AE的长．
解答：解：∵∠C=90°，AC=6，BC=8，
∴AC=10，
∵将△ABC绕点B旋转90°，
∴∠DBE=90°，
∴AE=
=
=10
．
故选B．
∴AC=10，
∵将△ABC绕点B旋转90°，
∴∠DBE=90°，
∴AE=
| BE2+BD2 |
| 102+102 |
| 2 |
故选B．
点评：本题主要考查了旋转的性质以及勾股定理，难度适中．
练习册系列答案
相关题目
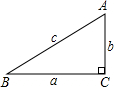如图，已知直角三角形ABC的三边分别为a、b、c，则sinA等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
21、根据下列语句作图、测量和比较．
已知直角三角形ABC中，∠C=90°，BC=6，CA=3，CD为∠C的角平分线，则CD=