题目内容
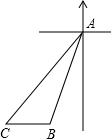 如图,一船在A处看见灯塔B在它的南偏西30°的方向,这时船和灯塔的距离为40海里,然后船向西南方向船行到C处,这时望见灯塔B在它的正东方向,问船航行了多少海里?(不取近似值)
如图,一船在A处看见灯塔B在它的南偏西30°的方向,这时船和灯塔的距离为40海里,然后船向西南方向船行到C处,这时望见灯塔B在它的正东方向,问船航行了多少海里?(不取近似值)
分析:本题要求的是AC的值,可通过构造直角三角形来解答,延长CB交AM于D,AD为直角三角形ABD和ACD的公共直角边,可先通过求AD的值来求AC的长.
解答: 解:延长CB交AM于D,
解:延长CB交AM于D,
∵Rt△ABD中,∠BAD=30°,AB=40,
∴AD=AB•cos30°=20
.
∵船在A点向西南方向船行到C处,
∴∠CAD=45°,
∴∠C=90°-45°=45°,AD=20
,
∴AC=AD÷sin45°=
AD=20
.
因此这时船航行了20
海里.
 解:延长CB交AM于D,
解:延长CB交AM于D,∵Rt△ABD中,∠BAD=30°,AB=40,
∴AD=AB•cos30°=20
| 3 |
∵船在A点向西南方向船行到C处,
∴∠CAD=45°,
∴∠C=90°-45°=45°,AD=20
| 3 |
∴AC=AD÷sin45°=
| 2 |
| 6 |
因此这时船航行了20
| 6 |
点评:本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,使问题解决,有公共的直角边的一般先求出这条直角边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
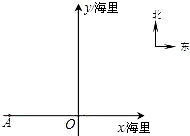 分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上.
分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上.


 如图,一船在A处看见灯塔B在它的南偏西30°的方向,这时船和灯塔的距离为40海里,然后船向西南方向船行到C处,这时望见灯塔B在它的正东方向,问船航行了多少海里?(不取近似值)
如图,一船在A处看见灯塔B在它的南偏西30°的方向,这时船和灯塔的距离为40海里,然后船向西南方向船行到C处,这时望见灯塔B在它的正东方向,问船航行了多少海里?(不取近似值)