Question

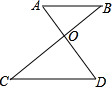如图，已知∠A=∠D，AD、BC交于点O．
（1）试说明△AOB∽△DOC．
（2）若AO=2，DO=3，CD=5，求AB的长．

Answer 1

分析：（1）△AOB、△DOC中，已知了∠A=∠D，且对顶角∠AOB=∠COD，两组对应角相等，可判定两个三角形相似；
（2）根据（1）的相似三角形得出的成比例线段，可求出AB的长．

解答：（1）证明：∵∠A=∠D，∠AOB=∠DOC，
∴△AOB∽△DOC；

（2）解：由（1）得：

OA

OD

=

AB

CD

；
∴AB=

OA•CD

OD

=

2×5

3

=

10

3

．

点评：此题主要考查的是相似三角形的判定和性质：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似（AA）；相似三角形的对应边成比例．