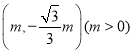题目内容
【题目】函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数,
为常数,![]() 与
与![]() 合起来的图象记为
合起来的图象记为![]() .
.
(Ⅰ)若![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)若![]() 的顶点在直线
的顶点在直线![]() 上,求
上,求![]() 的值;
的值;
(Ⅲ)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)将点C的坐标代入![]() 的解析式即可求出m的值;
的解析式即可求出m的值;
(Ⅱ)先求出抛物线![]() 的顶点坐标,再根据顶点在直线
的顶点坐标,再根据顶点在直线![]() 上得出关于m的方程,解之即可
上得出关于m的方程,解之即可
(Ⅲ)先求出抛物线![]() 的顶点坐标,结合(Ⅱ)抛物线
的顶点坐标,结合(Ⅱ)抛物线![]() 的顶点坐标,和x的取值范围,分三种情形讨论求解即可;
的顶点坐标,和x的取值范围,分三种情形讨论求解即可;
解:(Ⅰ)将点![]() 代入
代入![]() 的解析式,解得
的解析式,解得![]()
(Ⅱ)抛物线![]() 的顶点坐标为
的顶点坐标为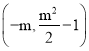 ,
,
令![]() ,得
,得![]()
∵![]() ,∴
,∴![]()
(Ⅲ)∵抛物线![]() 的顶点
的顶点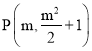 ,抛物线
,抛物线![]() 的顶点
的顶点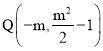 ,
,
当![]() 时,最高点是抛物线G1的顶点
时,最高点是抛物线G1的顶点
∴![]() ,解得
,解得![]()
当![]() 时,G1中(2,2m-1)是最高点,
时,G1中(2,2m-1)是最高点,![]() 2m-1
2m-1
∴![]() 2m-1
2m-1![]() ,解得
,解得![]()
当![]() 时,G2中(-4,4m-9)是最高点,
时,G2中(-4,4m-9)是最高点,![]() 4m-9.
4m-9.
∴![]() 4m-9
4m-9![]() ,解得
,解得![]() .
.
综上所述,![]() 即为所求.
即为所求.

练习册系列答案
相关题目