题目内容
 已知AB∥CD,此时∠A、∠AEF、∠EFC和∠C的关系如何?
已知AB∥CD,此时∠A、∠AEF、∠EFC和∠C的关系如何?考点:平行线的性质
专题:
分析:首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,可得AB∥EM∥FN∥CD,然后由两直线平行,同旁内角互补,求得∠A+∠1=180°,∠2+∠3=180°,∠4+∠C=180°,继而求得答案.
解答: 解:∠A+∠AEF+∠EFC+∠C=540°.
解:∠A+∠AEF+∠EFC+∠C=540°.
理由:过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴AB∥EM∥FN∥CD,
∴∠A+∠1=180°,∠2+∠3=180°,∠4+∠C=180°,
∴∠A+∠AEF+∠EFC+∠C=∠A+∠1+∠2+∠3+∠4+∠C=540°.
 解:∠A+∠AEF+∠EFC+∠C=540°.
解:∠A+∠AEF+∠EFC+∠C=540°.理由:过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴AB∥EM∥FN∥CD,
∴∠A+∠1=180°,∠2+∠3=180°,∠4+∠C=180°,
∴∠A+∠AEF+∠EFC+∠C=∠A+∠1+∠2+∠3+∠4+∠C=540°.
点评:此题考查了平行线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
一个多边形的内角和是外角和的3倍,则这个多边形是( )
| A、五边形 | B、六边形 |
| C、七边形 | D、八边形 |
a、b是两个有理数,若a-b<0,那么关于a、b的说法一定正确的是( )
| A、a<0,b<0 |
| B、a<0,b>0 |
| C、a>0,b<0 |
| D、a<b |
下列图形中,正确表示△ABC中BC边上的高的是( )
A、 |
B、 |
C、 |
D、 |
某三角形的三个内角之比为6:2:1,该三角形的形状是( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |
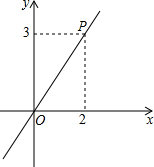 如图,已知正比例函数y=kx经过点P,
如图,已知正比例函数y=kx经过点P, 如图,直线a、b、c被直线l所截,如果∠1=∠2=65°,且直线b∥c,那么直线a与c平行吗?∠3等于多少度?
如图,直线a、b、c被直线l所截,如果∠1=∠2=65°,且直线b∥c,那么直线a与c平行吗?∠3等于多少度? 如图,将边长为a小正方形与边长为b的大正方形放在一起(b>a>0),用a、b表示△ABC的面积;
如图,将边长为a小正方形与边长为b的大正方形放在一起(b>a>0),用a、b表示△ABC的面积;