题目内容
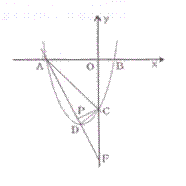
29.如图 ,已知抛物线y=ax2+bx+c与x轴交于点A、B ,与直线AC:y=-x-6交y轴于点C、D,点D是抛物线
的顶点 ,且横坐标为-2.
(1)求出抛物线的解析式。
(2)判断△ACD的形状,并说明理由。
(3)直线AD交y轴于点F ,在线段AD上是否存在一点P ,使∠ADC=∠PCF .若存在 ,直接写出点P的坐标;若不存在,说明理由。
练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
在平面直角坐标系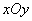 中,
中, 的半径为r,P是与圆心C不重合的点,点P关于
的半径为r,P是与圆心C不重合的点,点P关于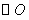 的反称点的定义如下:若
的反称点的定义如下:若 在射线CP上存在一点
在射线CP上存在一点 ,满足
,满足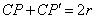 ,则称
,则称 为点P关于
为点P关于 的反称点,下图为点P及其
的反称点,下图为点P及其 关于
关于 的反称点
的反称点 的示意图。
的示意图。
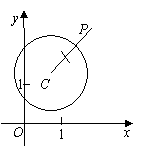 |
(1)当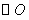 的半径为1时。
的半径为1时。
①分别判断点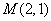 ,
,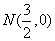 ,
,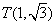 关于
关于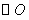 的反称点是否存在,若存
的反称点是否存在,若存 在?
在?
求其坐标;
②点P在直线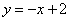 上,若点P关于
上,若点P关于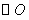 的反称点
的反称点 存在,且点
存在,且点 不在x轴上,求点P的横坐标的取值范围;
不在x轴上,求点P的横坐标的取值范围;
(2)当 的圆心在x轴上,半径为1,直线
的圆心在x轴上,半径为1,直线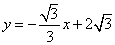 与x轴,y轴分别交于点A,B,若线段AB上存在点P,使得点P关于
与x轴,y轴分别交于点A,B,若线段AB上存在点P,使得点P关于 的反称点
的反称点 在
在 的内部,求圆心C的横坐标的取值范围。
的内部,求圆心C的横坐标的取值范围。


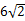 ,其中正确判断的序号是( )
,其中正确判断的序号是( )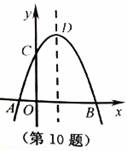
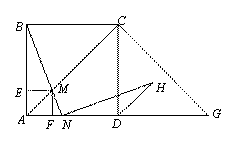

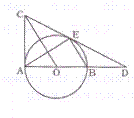 (1)求证:AC是⊙O的切线 ; (2)若BD=OB=4 ,求弦AE的长。
(1)求证:AC是⊙O的切线 ; (2)若BD=OB=4 ,求弦AE的长。 3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为
3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为 .56°
.56°

 上,作RT⊿ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若⊿BCE的面积为8,则k= 。
上,作RT⊿ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若⊿BCE的面积为8,则k= 。