题目内容
 如图所示,⊙O的半径为10cm,在⊙O中,直径AB与CD垂直,以点B为圆心,BC为半径的扇形CBD的面积是多少?
如图所示,⊙O的半径为10cm,在⊙O中,直径AB与CD垂直,以点B为圆心,BC为半径的扇形CBD的面积是多少?
分析:由图知,扇形ADB的圆心角为90度,△CBD是等腰直角三角形,由勾股定理可得,BC=BD=
OC,根据扇形的面积公式S=
求解.
| 2 |
| nπR2 |
| 360 |
解答:解:∵OC=OB=10cm,OC⊥OB,∠BOC=90°,
∴BC=
=10
cm,∠OBC=45度.
∴∠CBD=2∠OBC=90°,
S扇形BCD=
=50πcm2.
∴BC=
| OB2+OC2 |
| 2 |
∴∠CBD=2∠OBC=90°,
S扇形BCD=
90π×(10
| ||
| 360 |
点评:本题利用了等腰直角三角形的性质,勾股定理,扇形的面积公式求解.

练习册系列答案
相关题目
 37、如图所示,⊙O的半径为5,点P为⊙O外一点,OP=8cm.
37、如图所示,⊙O的半径为5,点P为⊙O外一点,OP=8cm.
 如图所示,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移
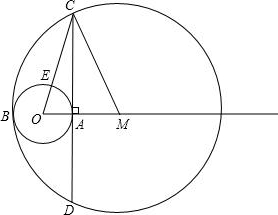
如图所示,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移 如图所示,⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,且sin∠CBD=
如图所示,⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,且sin∠CBD=