题目内容
如果点A、B、C、D的坐标依次为A（3，2）、B（3，-2）、C（-3，-2）、D（-3，0），则四边形ABCD的面积是________．
18
分析：把点A、B、C、D在平面直角坐标系中标出，然后根据梯形的面积公式进行计算．
解答：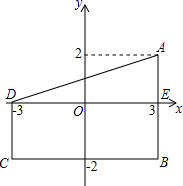
解：如图，A（3，2）、B（3，-2）、C（-3，-2）、D（-3，0）．
则四边形ABCD是直角梯形，且AB=4，DE=6，CD=2，
所以，S四边形ABCD=
（DC+AB）•DE=×（2+4）×6=18．
故答案是：18．
点评：本题考查了三角形的面积，坐标与图形性质．根据所给点的坐标推知四边形ABCD是直角梯形是解题的关键．
分析：把点A、B、C、D在平面直角坐标系中标出，然后根据梯形的面积公式进行计算．
解答：
解：如图，A（3，2）、B（3，-2）、C（-3，-2）、D（-3，0）．则四边形ABCD是直角梯形，且AB=4，DE=6，CD=2，
所以，S四边形ABCD=
（DC+AB）•DE=×（2+4）×6=18．故答案是：18．
点评：本题考查了三角形的面积，坐标与图形性质．根据所给点的坐标推知四边形ABCD是直角梯形是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如果点P在坐标轴上，以P为圆心，
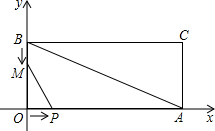时（0≤x≤12），△POM的面积为y．
EG垂直于y轴，垂足为G，过点C作CF垂直于y轴，垂足为F，连接DE．