题目内容
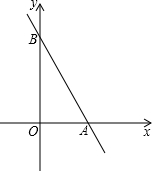如果点P在坐标轴上，以P为圆心，| 3 |
| 3 |
| 3 |
分析：由直线解析式可知，OA=2，OB=2
，由面积法知△OAB边AB上的高正好是所求圆的半径，故点O是所求的点，再满足题意的点关于点A成中心对称图形，故点O关于点A的对称点、点O关于点B的对称点也满足题意．
| 3 |
解答：
解：过点O作直线AB的垂线，垂足为C点，
由直线解析式可知：OA=2，OB=2
，
由勾股定理可知：AB=4，
由面积法可知，OC•AB=OA•OB，
∴OC=
，故原点O（0，0）满足题意；
由于OA=2，OB=2
，根据中心对称性得点（4，0）、（0，4
）满足题意．
故本题答案为：（0，0），（4，0），（0，4
）．
解：过点O作直线AB的垂线，垂足为C点，由直线解析式可知：OA=2，OB=2
| 3 |
由勾股定理可知：AB=4，
由面积法可知，OC•AB=OA•OB，
∴OC=
| 3 |
由于OA=2，OB=2
| 3 |
| 3 |
故本题答案为：（0，0），（4，0），（0，4
| 3 |
点评：本题是直线与圆的位置关系在直角坐标系的运用，通过巧妙设计点到直线的距离求解．
练习册系列答案
阅读快车系列答案
相关题目
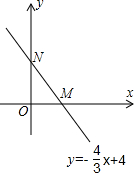如图，直线y=-
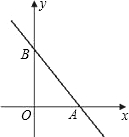如果点P在坐标轴上，以点P为圆心，
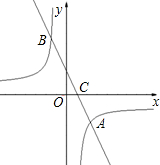C，如果点D在坐标轴上，且OA=DC．