题目内容
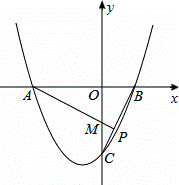
如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
(1)若x2=1,BC=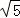 ,求函数y=x2+bx+c的最小值;
,求函数y=x2+bx+c的最小值;
(2)过点A作AP⊥BC,垂足为P(点P在线段BC上),AP交y轴于点M.若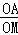 =2,求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.
=2,求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.


解:(1)∵x2=1,BC=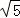 ,
,
∴OC= =2,
=2,
∴C(0,﹣2),
把B(1,0),C(0,﹣2)代入y=x2+bx+c,得:0=1+b﹣2,
解得:b=1,
∴抛物线的解析式为:y=x2+x+﹣2.
转化为y=(x+ )2﹣
)2﹣ ;
;
∴函数y=x2+bx+c的最小值为﹣ .
.
(2)∵∠OAM+∠OBC=90°,∠OCB+∠OBC=90°,
∴∠OAM=∠OCB,又∵∠AOM=∠BOC=90°,
∴△AOM∽△COB,
∴ ,
,
∴OC= •OB=2OB,
•OB=2OB,
∴﹣c=2x2,即x2=﹣ .
.
∵x22+bx2+c=0,将x2=﹣ 代入化简得:c=2b﹣4.
代入化简得:c=2b﹣4.
抛物线的解析式为:y=x2+bx+c,其顶点坐标为(﹣ ,
, ).
).
令x=﹣ ,则b=﹣2x.
,则b=﹣2x.
y= =c﹣
=c﹣ =2b﹣4﹣
=2b﹣4﹣ =﹣4x﹣4﹣x2,
=﹣4x﹣4﹣x2,
∴顶点的纵坐标随横坐标变化的函数解析式为:y=﹣x2﹣4x﹣4(x>﹣ ).
).



练习册系列答案
相关题目
 ,则
,则 的值为______.
的值为______. B.
B.  C.
C.  D. 1
D. 1 )0﹣(8﹣2)
)0﹣(8﹣2)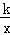 图象上的两点,且x1﹣x2=﹣2,x1•x2=3,y1﹣y2=﹣
图象上的两点,且x1﹣x2=﹣2,x1•x2=3,y1﹣y2=﹣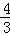 ,当﹣3<x<﹣1时,求y的取值范围.
,当﹣3<x<﹣1时,求y的取值范围.
