题目内容
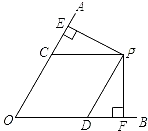
 如图,点P是∠AOB的角平分线上一点,过点P作PC∥OA交OB于点C,过点P作PD⊥OA于点D,若∠AOB=60°,OC=4,则PD=
如图,点P是∠AOB的角平分线上一点,过点P作PC∥OA交OB于点C,过点P作PD⊥OA于点D,若∠AOB=60°,OC=4,则PD=分析:在△OCP中,由题中所给的条件可求出OP的长,根据直角三角形的性质可知,在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半,故PD=
OP.
| 1 |
| 2 |
解答: 解:∵∠AOB=60°,点P是∠AOB的角平分线上一点,
解:∵∠AOB=60°,点P是∠AOB的角平分线上一点,
∴∠POD=∠POC=30°,
又∵PC∥OA,
∴∠PCB=60°,∴∠POC=30°,
∵∠PCB=180°-∠60°=120°,
∴∠POC=∠OPC,
∴△OCP为等腰三角形,
∵OC=4,∠PCE=60°,
∴PC=4,CE=2,PE=
=2
,
可求OP=4
,
又∵PD=
OP,
∴PD=2
.
故答案为2
.
 解:∵∠AOB=60°,点P是∠AOB的角平分线上一点,
解:∵∠AOB=60°,点P是∠AOB的角平分线上一点,∴∠POD=∠POC=30°,
又∵PC∥OA,
∴∠PCB=60°,∴∠POC=30°,
∵∠PCB=180°-∠60°=120°,
∴∠POC=∠OPC,
∴△OCP为等腰三角形,
∵OC=4,∠PCE=60°,
∴PC=4,CE=2,PE=
| 4 2-22 |
| 3 |
可求OP=4
| 3 |
又∵PD=
| 1 |
| 2 |
∴PD=2
| 3 |
故答案为2
| 3 |
点评:本题主要考查角平分线和等腰三角形的判定及计算技巧.借助于角平分线和等腰三角形求解角的度数和边长从而求得最后结果.

练习册系列答案
相关题目
 63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中:
63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中: 24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
 PF⊥OB,垂足分别为点E、F.
PF⊥OB,垂足分别为点E、F. 如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是
如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是