题目内容
有一个正在向上移动的自动电梯,A从其顶端往下走到它的底端,共计走了150级.B从其底端往上走到它的顶端,共计走了75级,假定A的速度(单位时间走的级数)是B的速度的3倍,那么在任何一个时刻可见到的自动电梯的级数是多少(假定此数是常数)________.
120
分析:A的速度是B的3倍,则A走150级=B走50级(时间).所以A下楼时间:B上楼时间= :
: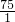 =2:3.所以A下楼时:扶梯长出级数=
=2:3.所以A下楼时:扶梯长出级数= B上楼时扶梯长出级数.故设A下楼长出x级,则B上楼缩减
B上楼时扶梯长出级数.故设A下楼长出x级,则B上楼缩减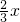 级,扶梯静长y级,根据A下楼与B下楼列出等量关系式求解.
级,扶梯静长y级,根据A下楼与B下楼列出等量关系式求解.
解答:设A下楼长出x级,则B上楼缩减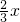 级,扶梯静长y级,
级,扶梯静长y级,
A下楼:150=y+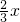 ,
,
B上楼:75=y-x,
解得 y=120级.
故答案为:120级.
点评:本题考查分式方程的应用.解决本题的关键是根据题目说明,找准甲下楼长出级数与乙上楼缩减级数间的比例关系,从而建立等量关系,解得结果.
分析:A的速度是B的3倍,则A走150级=B走50级(时间).所以A下楼时间:B上楼时间=
 :
: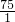 =2:3.所以A下楼时:扶梯长出级数=
=2:3.所以A下楼时:扶梯长出级数= B上楼时扶梯长出级数.故设A下楼长出x级,则B上楼缩减
B上楼时扶梯长出级数.故设A下楼长出x级,则B上楼缩减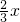 级,扶梯静长y级,根据A下楼与B下楼列出等量关系式求解.
级,扶梯静长y级,根据A下楼与B下楼列出等量关系式求解.解答:设A下楼长出x级,则B上楼缩减
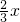 级,扶梯静长y级,
级,扶梯静长y级,A下楼:150=y+
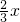 ,
,B上楼:75=y-x,
解得 y=120级.
故答案为:120级.
点评:本题考查分式方程的应用.解决本题的关键是根据题目说明,找准甲下楼长出级数与乙上楼缩减级数间的比例关系,从而建立等量关系,解得结果.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目