题目内容
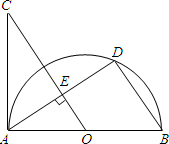 如图,AB是半圆O的直径,AC是⊙O的切线,过点O作弦AD的垂线交弦AD于点E,交AC 于点C.若OC=20,AB=24.
如图,AB是半圆O的直径,AC是⊙O的切线,过点O作弦AD的垂线交弦AD于点E,交AC 于点C.若OC=20,AB=24.
(1)求证:∠B=∠AOC.
(2)求DB的长.
(1)证明:∵AB为半圆O的直径,
∴∠ADB=90°,
∵CO⊥AD,
∴∠AEO=90°,
∴∠ADB=∠AEO,
∴CO∥DB,
∴∠B=∠AOC;
(2)解:∵AB为半圆O的直径,AC为圆O的切线,
∴∠ADB=∠CAO=90°,
∵∠B=∠AOC,
∴△CAO∽△ADB,
∴ =
= ,
,
∵OC=20,AB=24,
∴OA=12,
∴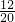 =
=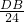 ,
,
则DB= .
.
分析:(1)由AB为半圆O的直径,利用直径所对的圆周角为直角得到∠ADB=90°,再由CO⊥AD,利用垂直定义得到一对同位角相等,利用同位角相等两直线平行得到CO∥DB,再利用两直线平行同位角相等即可得证;
(2)AC为圆O的切线,利用切线的性质得到CA垂直于AB,进而得到一对直角相等,再由(1)得到一对角相等,利用两对对应角相等的两三角形相似得到三角形ACO与三角形ABD相似,由相似得比例,将各自的值代入计算即可求出DB的长.
点评:此题考查了切线的性质,相似三角形的判定与性质,平行线的判定与性质,以及圆周角定理,熟练掌握切线的性质是解本题的关键.
∴∠ADB=90°,
∵CO⊥AD,
∴∠AEO=90°,
∴∠ADB=∠AEO,
∴CO∥DB,
∴∠B=∠AOC;
(2)解:∵AB为半圆O的直径,AC为圆O的切线,
∴∠ADB=∠CAO=90°,
∵∠B=∠AOC,
∴△CAO∽△ADB,
∴
 =
= ,
,∵OC=20,AB=24,
∴OA=12,
∴
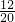 =
=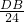 ,
,则DB=
 .
.分析:(1)由AB为半圆O的直径,利用直径所对的圆周角为直角得到∠ADB=90°,再由CO⊥AD,利用垂直定义得到一对同位角相等,利用同位角相等两直线平行得到CO∥DB,再利用两直线平行同位角相等即可得证;
(2)AC为圆O的切线,利用切线的性质得到CA垂直于AB,进而得到一对直角相等,再由(1)得到一对角相等,利用两对对应角相等的两三角形相似得到三角形ACO与三角形ABD相似,由相似得比例,将各自的值代入计算即可求出DB的长.
点评:此题考查了切线的性质,相似三角形的判定与性质,平行线的判定与性质,以及圆周角定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm. 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
