题目内容
如图所示,△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若∠DEF=52°,则∠A的度数是

76°.
【解析】
试题分析:连接OD、OF;由圆周角定理可求得∠DOF的度数;在四边形ADOF中,∠ODA=∠OFA=90°,因此∠A和∠DOF互补,由此可求出∠A的度数.
试题解析:连接OD,OF,则∠ADO=∠AFO=90°;

由圆周角定理知,∠DOF=2∠E=104°;
∴∠A=180°-∠DOF=76°.
考点:1三角形的内切圆与内心;2.圆周角定理;3.切线的性质.

练习册系列答案
相关题目
 B.
B. C.
C. D.
D.

 D、
D、


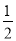 . 其中正确的说法是( )
. 其中正确的说法是( )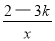 的图象的每一条曲线上,y都随x的增大而增大,写出一个符合题意的k的值 。
的图象的每一条曲线上,y都随x的增大而增大,写出一个符合题意的k的值 。