题目内容
13.如图1,二次函数y=ax2+bx+6(a≠0)的图象交y轴于C点,交x轴于A,B两点(点A在点B的左侧),tan∠CAB=3,tan∠CBA=1,(1)求出点A、点B的坐标及该二次函数表达式.
(2)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合),过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当m为何值时,△CDQ面积S最大,并求出最大值.
(3)如图3,线段MN是直线y=x上的动线段(点M在点N左侧),且MN=$\sqrt{2}$,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.

分析 (1)首先根据函数的解析式求得点C的坐标,然后根据tan∠CAB=3,tan∠CBA=1可求A、B两点坐标;将A、B两点坐标代入二次函数y=ax2+bx+6,可求二次函数解析式;
(2)由DQ∥AC得△BDQ∽△BCA,利用相似比表示△BDQ的面积,利用三角形面积公式表示△ACQ的面积,根据S△CDQ=S△ABC-S△BDQ-S△ACQ,运用二次函数的性质求面积最大时,m的值;
(3)以点P,M,Q,N为顶点的四边形能为平行四边形,因为M,N的位置不确定,所以要分三种情况讨论,求出满足题意的n值即可.
解答 解:(1)∵二次函数y=ax2+bx+6(a≠0)的图象交y轴于C点,
∴C(0,6),
∴OC=6,
∵tan∠CAB=3,tan∠CBA=1,
∴AO=2,BO=6,
∴A(-2,0)、B(6,0),
将A、B两点坐标代入二次函数y=ax2+bx+6,得
$\left\{\begin{array}{l}{4a-2b+6=0}\\{36a+6b+6=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
故y=-$\frac{1}{2}$x2+2x+6;
(2)依题意,得AB=8,QB=6-m,AQ=m+2,OC=6,则S△ABC=$\frac{1}{2}$AB×OC=24,
∵由DQ∥AC,
∴△BDQ∽△BCA,
$\frac{{S}_{△BDQ}}{{S}_{△BCA}}$=($\frac{BQ}{BA}$)2=($\frac{6-m}{8}$)2,
即S△BDQ=$\frac{3}{8}$(m-6)2,
又∵S△ACQ=$\frac{1}{2}$AQ×OC=3m+6,
∴S=S△ABC-S△BDQ-S△ACQ=24-$\frac{3}{8}$(m-6)2-(3m+6)=-$\frac{3}{8}$m2+$\frac{3}{2}$m+$\frac{9}{2}$=-$\frac{3}{8}$(m-2)2+6,
∴当m=2时,S最大;
(3)∵MN=$\sqrt{2}$,点A,B都在直线y=x上,MN在直线AB上,MN在线段 AB上,M的横坐标为n,纵坐标也为n,
如图3,过点M作x轴的平行线,过点N作y轴的平行线,它们相交于点H.
∴△MHN是等腰直角三角形.
∴MH=NH=1.
∴点N的坐标为(n+1,n+1),
①如图4,当n>0时,PM=n,
NQ=n+1-[-$\frac{1}{2}$(n+1)2+2(n+1)+6],
当四边形PMQN为平行四边形时,PM=NQ.
则n=n+1-[-$\frac{1}{2}$(n+1)2+2(n+1)+6],
解得n=-1+$\sqrt{14}$或$\sqrt{14}$-1;
②如图5,当n<0时,PM=-m,
NQ=n+1-[-$\frac{1}{2}$(n+1)2+2(n+1)+6],
当四边形PMQN为平行四边形时,PM=NQ.
则-n=n+1-[-$\frac{1}{2}$(n+1)2+2(n+1)+6],
解得n=1-$\sqrt{14}$或n=-1-$\sqrt{14}$,
③∵直线AB过O,即直线经过第一、三象限,
∴点M在第3象限点N在第2象限不存在;
综上所述以点P,M,Q,N为顶点的四边形能为平行四边形,n的值是n=1±$\sqrt{14}$,或n=-1±$\sqrt{14}$.
点评 本题考查了二次函数性质的综合运用、用待定系数法求出二次函数的解析式和平行四边形的判定和性质以及相似三角形的性质和判定既数学分类讨论思想的运用,题目的综合性强,难度大,能够很好的锻炼学生的解题能力.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案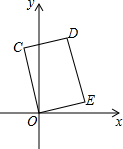 如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )| A. | 3 | B. | $2\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 4 |
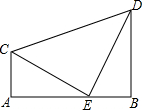 如图,E为线段AB上一点,AC⊥AB,DB⊥AB,△ACE≌△BED.
如图,E为线段AB上一点,AC⊥AB,DB⊥AB,△ACE≌△BED.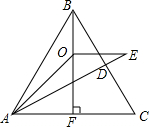 如图,在等边△ABC中,D是BC上任一点,延长AD至E,使AE=AB,作∠BAE的平分线交△ABC的高BF于O点,求∠AEO的度数.
如图,在等边△ABC中,D是BC上任一点,延长AD至E,使AE=AB,作∠BAE的平分线交△ABC的高BF于O点,求∠AEO的度数. 如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为2或32.
如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为2或32. 在平面直角坐标系中,一个二次函数的图象经过点A(1,0)、B(3,0)两点.
在平面直角坐标系中,一个二次函数的图象经过点A(1,0)、B(3,0)两点.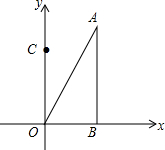 如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.
如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3$\sqrt{3}$),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.