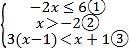��Ŀ����
����Ŀ����ͼ��P���߶�AB��һ�㣬C��D����ֱ��P��B������1cm/s��2 cm/s���ٶ���ֱ��AB�����˶���C���߶�AP�ϣ�D���߶�BP�ϣ�
(1)��C��D�˶�����һʱ��ʱ������PD��2AC����˵��P�����߶�AB�ϵ�λ�ã� ![]()
(2)��(1)�������£�Q��ֱ��AB��һ�㣬��AQ��BQ=PQ����![]() ��ֵ��
��ֵ��
![]()
(3)��(1)�������£���C��D�˶�5���ǡ����![]() ����ʱC��ֹͣ�˶���D������˶���D�����߶�PB�ϣ���M��N�ֱ���CD��PD���е㣬���н��ۣ���PM��PN��ֵ���䣻��
����ʱC��ֹͣ�˶���D������˶���D�����߶�PB�ϣ���M��N�ֱ���CD��PD���е㣬���н��ۣ���PM��PN��ֵ���䣻��![]() ��ֵ���䣬����˵����ֻ��һ����������ȷ�ģ������ҳ���ȷ�Ľ��۲���ֵ.
��ֵ���䣬����˵����ֻ��һ����������ȷ�ģ������ҳ���ȷ�Ľ��۲���ֵ.
���𰸡���1����P���߶�AB�ϵ�![]() ������2��
������2��![]() ����3����
����3����![]() ��ֵ����.
��ֵ����.
��������
��1������C��D���˶��ٶ�֪BD=2PC��������֪����PD=2AC���PB=2AP�����Ե�P���߶�AB�ϵ�![]() ����
����
��2�������軭��ͼʾ������AQ-BQ=PQ���AQ=PQ+BQ��Ȼ�����AP=BQ���Ӷ����PQ��AB�Ĺ�ϵ��
��3������Cֹͣ�˶�ʱ����CD��![]() AB���Ӷ����CM��AB��������ϵ��Ȼ�������AB��ʾ��PM��PN��ֵ������MN��PNPM��
AB���Ӷ����CM��AB��������ϵ��Ȼ�������AB��ʾ��PM��PN��ֵ������MN��PNPM��![]() AB��
AB��
�⣺��1�������⣺BD=2PC
��PD=2AC��
��BD+PD=2��PC+AC������PB=2AP.
���P���߶�AB�ϵ�![]() ����
����
��2����ͼ��
![]()
��AQ-BQ=PQ��
��AQ=PQ+BQ��
��AQ=AP+PQ��
��AP=BQ��
��PQ=![]() AB��
AB��
��![]()
��3����![]() ��ֵ����.
��ֵ����.
���ɣ���ͼ��
![]()
����Cֹͣ�˶�ʱ����CD=![]() AB��
AB��
��CM=![]() AB��
AB��
��PM=CM-CP=![]() AB-5��
AB-5��
��PD=![]() AB-10��
AB-10��
��PN=![]() AB-10��=
AB-10��=![]() AB-5��
AB-5��
��MN=PN-PM=![]() AB��
AB��
����Cֹͣ�˶���D������˶�ʱ��MN��ֵ���䣬
����![]() .
.