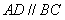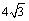题目内容
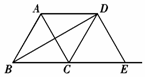
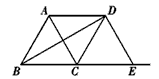
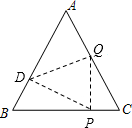 如图△ABC是边长为2的等边三角形,D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.
如图△ABC是边长为2的等边三角形,D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.
分析:作出D关于BC、AC的对称点D'、D'',连接D'D'',DQ,DP,根据轴对称的性质将三角形的周长最值问题转化为两点之间线段最短的问题,利用等边三角形的性质和三角函数即可解答.
解答: 解:作D关于BC、AC的对称点D'、D'',连接D'D'',DQ,DP.
解:作D关于BC、AC的对称点D'、D'',连接D'D'',DQ,DP.
∵DQ=D''Q,DP=D'P,
∴△DPQ的周长为PQ+DQ+DP=PQ+D''Q+D'P=D'D'',
根据两点之间线段最短,D'D''的长即为三角形周长的最小值.
∵∠A=∠B=60°,∠BED=∠AFD=90°,
∴∠α=∠β=90°-60°=30°,
∠D'DD''=180°-30°-30°=120°,
∵D为AB的中点,
∴DF=AD•cos30°=1×
=
,AF=
,
易得△ADF≌△QD''F,
∴QF=AF=
,
∴AQ=1,BP=1,
Q、P为AC、BC的中点.
∴DD''=
×2=
,
同理,DD'=
×2=
,
∴△DD'D''为直角三角形,
∴∠D'=∠D''=
=30°,
∴D''D'=2DD'•cos30°=2×
×
=3.
 解:作D关于BC、AC的对称点D'、D'',连接D'D'',DQ,DP.
解:作D关于BC、AC的对称点D'、D'',连接D'D'',DQ,DP.∵DQ=D''Q,DP=D'P,
∴△DPQ的周长为PQ+DQ+DP=PQ+D''Q+D'P=D'D'',
根据两点之间线段最短,D'D''的长即为三角形周长的最小值.
∵∠A=∠B=60°,∠BED=∠AFD=90°,
∴∠α=∠β=90°-60°=30°,
∠D'DD''=180°-30°-30°=120°,
∵D为AB的中点,
∴DF=AD•cos30°=1×
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
易得△ADF≌△QD''F,
∴QF=AF=
| 1 |
| 2 |
∴AQ=1,BP=1,
Q、P为AC、BC的中点.
∴DD''=
| ||
| 2 |
| 3 |
同理,DD'=
| ||
| 2 |
| 3 |
∴△DD'D''为直角三角形,
∴∠D'=∠D''=
| 180°-120° |
| 2 |
∴D''D'=2DD'•cos30°=2×
| 3 |
| ||
| 2 |
点评:此题考查了轴对称--最短路径问题,涉及正三角形的性质、三角函数、三角形的内角和定理、等腰三角形的性质和判定等知识,有一定难度.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 已知:如图△ABC是边长为4的等边三角形,点P、Q分别从A、C两点同时出发,速度为每秒1个单位长度,B与原点重合,PQ交AC于D.
已知:如图△ABC是边长为4的等边三角形,点P、Q分别从A、C两点同时出发,速度为每秒1个单位长度,B与原点重合,PQ交AC于D. 如图△ABC是边长为2的等边三角形,D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.
如图△ABC是边长为2的等边三角形,D是AB边的中点,P是BC边上的动点,Q是AC边上的动点,当P、Q的位置在何处时,才能使△DPQ的周长最小?并求出这个最值.