题目内容
如图,在△ABC中,∠A=40°,有一块直角三角板DEF的两条直角边DE、DF分别经过点B、C,若直角顶点D在三角形外部,则∠ABD+∠ACD的度数是__________度.
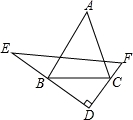
230度.
【考点】多边形内角与外角.
【分析】要求∠ABD+∠ACD的度数,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形内角和定理得出∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°;根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=90°,∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+90°=230°.
【解答】解:在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°﹣40°=140°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=90°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+90°=230°.
故答案为:230.
【点评】考查三角形内角和定理,外角性质.熟练掌握这些性质是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目


 和点D、E、F、G、H、K均在格点上,现以D、E、F、G、H、K中的三个点为顶点画三角形.
和点D、E、F、G、H、K均在格点上,现以D、E、F、G、H、K中的三个点为顶点画三角形.
 C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.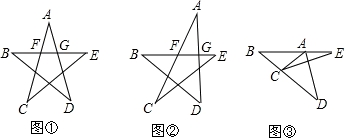
 ,
, ,
, ,且
,且 ,则
,则 00元.
00元. ,求y与x之间的函数关系式;
,求y与x之间的函数关系式;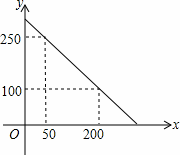 (3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种 方案能使获利最大?最大获利为多少元?
方案能使获利最大?最大获利为多少元?