题目内容
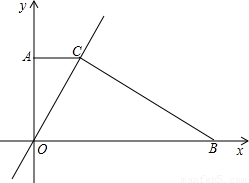
(2003•黑龙江)如图,某同学用一个有60°角的直角三角板估测学校旗杆AB的高度,他将60°角的直角边水平放在1.5米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5米,则旗杆AB的高度约为 米(精确到1米, 取1.73).
取1.73).
【答案】分析:在△ACE中,CE⊥AE,tan∠ACE= ,由此可以求出AE. AB=AE+BE=AE+CD.
,由此可以求出AE. AB=AE+BE=AE+CD.
解答:解:由题意可知,在△ACE中,CE⊥AE,且∠ACE=60°,BD=5,
而tan∠ACE= ,
,
∴ ≈8.6.
≈8.6.
又∵EB=1.5,
∴AB=AE+EB≈10(米).
点评:解题的关键是把实际问题抽象到解直角三角形中,然后利用三角函数的定义解决问题.
 ,由此可以求出AE. AB=AE+BE=AE+CD.
,由此可以求出AE. AB=AE+BE=AE+CD.解答:解:由题意可知,在△ACE中,CE⊥AE,且∠ACE=60°,BD=5,
而tan∠ACE=
 ,
,∴
 ≈8.6.
≈8.6.又∵EB=1.5,
∴AB=AE+EB≈10(米).
点评:解题的关键是把实际问题抽象到解直角三角形中,然后利用三角函数的定义解决问题.

练习册系列答案
相关题目
 S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.
S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.
 S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.
S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.