题目内容
(1)请证明不论a为何值,方程x2-(a-4)x-| 1 | 4 |
(2)请你选择一个你喜欢的a值,求出方程的实数根.
分析:(1)要证明不论a为何值,方程x2-(a-4)x-
=0总有两个不相等的实数根,就是要证明△>0.△=[-(a-4)]2-4×(-
)=(a-4)2+1,由(a-4)2≥0可得△>0;
(2)取a=4,方程变为x2-
=0,用直接开平方法解即可.
| 1 |
| 4 |
| 1 |
| 4 |
(2)取a=4,方程变为x2-
| 1 |
| 4 |
解答:解:(1)∵△=[-(a-4)]2-4×(-
)=(a-4)2+1,
而不论a为何值,总有(a-4)2≥0,
∴△>0,
所以不论a为何值,方程x2-(a-4)x-
=0总有两个不相等的实数根;
(2)取a=4,方程变为x2-
=0,
∴x2=
,
解得x1=
,x2=-
.
| 1 |
| 4 |
而不论a为何值,总有(a-4)2≥0,
∴△>0,
所以不论a为何值,方程x2-(a-4)x-
| 1 |
| 4 |
(2)取a=4,方程变为x2-
| 1 |
| 4 |
∴x2=
| 1 |
| 4 |
解得x1=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
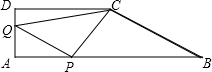 速度移动,如果P、Q同时出发,用t表示移动的时间(单位:秒),并且0≤t≤3.
速度移动,如果P、Q同时出发,用t表示移动的时间(单位:秒),并且0≤t≤3.
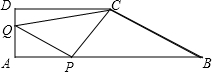 速度移动,如果P、Q同时出发,用t表示移动的时间(单位:秒),并且0≤t≤3.
速度移动,如果P、Q同时出发,用t表示移动的时间(单位:秒),并且0≤t≤3.