Question

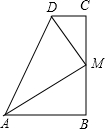如图，在梯形ABCD中，∠C=90°，M是BC的中点，DM平分∠ADC，∠CMD=35°，则∠MAB是

1. A.
   35°
2. B.
   55°
3. C.
   70°
4. D.
   20°

Answer 1

A
分析：根据角平分线性质得出EM=MC=BM，推出AM平分∠DAB，求出∠CDA即可求出答案．
解答：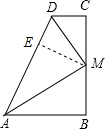
∵∠c=90°，∠CMD=35°，
∴∠cdm=55°，
∵DM平分∠CDA，
∴∠CAD=2∠CDM=110°，
∵DC∥AB，
∴∠DAB=180°-∠CDA=70°，
过M作ME⊥AD于E，
∵∠C=90°，DM平分∠ADC，
∴ME=MC，
∵M为BC中点，
∴BM=MC，
∴ME=MB，
∵DC∥AB，∠C=90°，
∴∠B=90°，
∴∠EAM=∠BAM=∠DAB=×70°=35°，
故选A．
点评：本题考查了角平分线性质，三角形的内角和定理，等腰三角形的性质的应用，注意：角平分线上的点到角的两边的距离相等．