题目内容
如图,在平面直角坐标系中,四边形ABCO是梯形,其中A(6,0),B(3, ),C(1,
),C(1, ),动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→ C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、Q运动的时间为t(秒).
),动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→ C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、Q运动的时间为t(秒).

(1)求经过A、B、C三点的抛物线的解析式;
(2)当点Q在CO边上运动时,求△OPQ的面积S与时间t的函数关系式;
(3)以O、P、Q为顶点的三角形能构成直角三角形吗?若能,请求出t的值,若不能,请说明理由;
(4)经过A、B、C三点的抛物线的对称轴、直线OB和PQ能够交于一点吗?若能,请求出此时t的值(或范围),若不能,请说明理由.
 ),C(1,
),C(1, ),动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→ C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、Q运动的时间为t(秒).
),动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→ C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、Q运动的时间为t(秒).
(1)求经过A、B、C三点的抛物线的解析式;
(2)当点Q在CO边上运动时,求△OPQ的面积S与时间t的函数关系式;
(3)以O、P、Q为顶点的三角形能构成直角三角形吗?若能,请求出t的值,若不能,请说明理由;
(4)经过A、B、C三点的抛物线的对称轴、直线OB和PQ能够交于一点吗?若能,请求出此时t的值(或范围),若不能,请说明理由.
(1)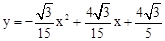 (2)
(2)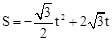 (2≤t≤3)(3)不能(4)能够交于一点,此时0≤t≤2
(2≤t≤3)(3)不能(4)能够交于一点,此时0≤t≤2
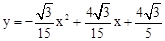 (2)
(2)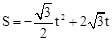 (2≤t≤3)(3)不能(4)能够交于一点,此时0≤t≤2
(2≤t≤3)(3)不能(4)能够交于一点,此时0≤t≤2解:(1)设经过A、B、C三点的抛物线的解析式为: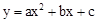 ,
,
把A(6,0),B(3,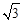 ),C(1,
),C(1,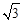 )代入得:
)代入得:
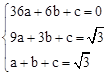 ,解得:
,解得: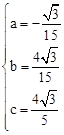 。
。
∴经过A、B、C三点的抛物线的解析式为: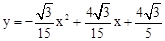 。
。
(2)∵可求BC=2,OC=2,OA=6
∴当点Q在CO边上运动,点P在OA边上运动时,2≤t≤3。
如图,过点C作CD⊥x轴的于点D,过点Q作QH⊥x轴的于点H,
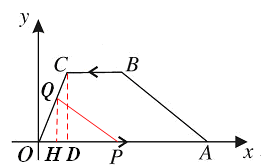
则OD=1,CD=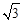 ,OC=2,
,OC=2,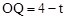 。
。
由△OQH∽△OCD得,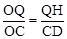 ,即
,即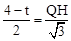 ,
,
∴ 。
。
又∵动点P的速度是每秒2个单位,∴OP=2t。
∴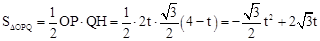 。
。
∴所求△OPQ的面积S与时间t的函数关系式为: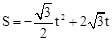 (2≤t≤3)。
(2≤t≤3)。
(3)根据题意可知,0≤t≤3。
当0≤t≤2时,点Q在BC边上运动,此时,OP=2t,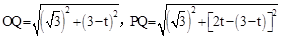 。
。
∵OD=1,CD=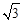 ,∴
,∴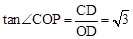 。∴
。∴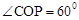 。
。
∵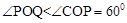 ,∴若△OPQ为直角三角形,只能是
,∴若△OPQ为直角三角形,只能是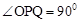 或
或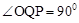 。
。
若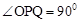 ,则
,则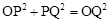 ,即
,即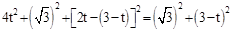 ,
,
解得, 或
或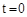 (舍去)。
(舍去)。
若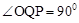 ,则
,则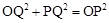 ,即
,即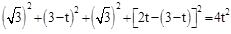 ,
,
解得,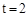 。
。
当2<t≤3时,点Q在CO边上运动,此时,OP=2t>4,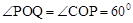 ,OQ<OC=2,
,OQ<OC=2,
∴此时,△OPQ不可能为直角三角形。
综上所述,当 或
或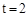 时,△OPQ为直角三角形。
时,△OPQ为直角三角形。
(4)由(1)可得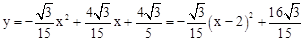 ,其对称轴为
,其对称轴为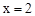 。
。
又直线OB的解析式为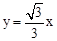 ,
,
∴抛物线对称轴与OB的交点为M(0,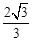 )。
)。
又P(2t,0),
设过点P、M的直线解析式为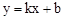 ,则
,则
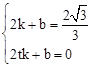 ,解得
,解得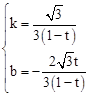 。
。
∴过点P、M的直线解析式为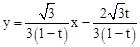 。
。
又当0≤t≤2时,Q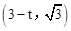 ,
,
把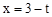 代入
代入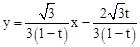 得
得
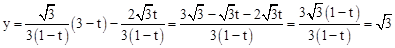 ,
,
∴点Q在直线PM上,即当0≤t≤2时,点P、M、Q总在一直线上。
当2<t≤3时,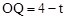 ,
,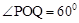 ,∴Q
,∴Q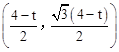 。
。
代入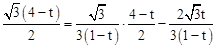 ,解得
,解得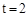 或
或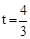 ,均不合题意,舍去。
,均不合题意,舍去。
综上所述,经过A、B、C三点的抛物线的对称轴、直线OB和PQ能够交于一点,此时0≤t≤2。
(1)应用待定系数法求解即可。
(2)过点C作CD⊥x轴的于点D,过点Q作QH⊥x轴的于点H,由△OQH∽△OCD得比例式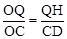 ,从而用t表示出△OPQ的边OP上的高
,从而用t表示出△OPQ的边OP上的高 ,进而根据三角形面积公式即可求得所求△OPQ的面积S与时间t的函数关系式。
,进而根据三角形面积公式即可求得所求△OPQ的面积S与时间t的函数关系式。
(3)分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论。
(4)根据二次函数的性质求出抛物线对称轴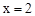 ,求出直线OB的解析式
,求出直线OB的解析式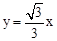 ,从而得到二者的交点
,从而得到二者的交点
M(0,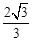 ),进而求出点P、M的直线解析式为
),进而求出点P、M的直线解析式为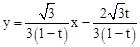 。分分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论点Q与直线
。分分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论点Q与直线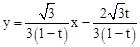 的关系,得出结论。
的关系,得出结论。
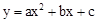 ,
,把A(6,0),B(3,
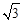 ),C(1,
),C(1,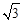 )代入得:
)代入得: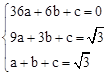 ,解得:
,解得: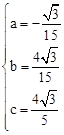 。
。∴经过A、B、C三点的抛物线的解析式为:
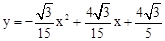 。
。(2)∵可求BC=2,OC=2,OA=6
∴当点Q在CO边上运动,点P在OA边上运动时,2≤t≤3。
如图,过点C作CD⊥x轴的于点D,过点Q作QH⊥x轴的于点H,

则OD=1,CD=
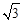 ,OC=2,
,OC=2,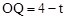 。
。由△OQH∽△OCD得,
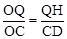 ,即
,即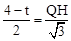 ,
,∴
 。
。又∵动点P的速度是每秒2个单位,∴OP=2t。
∴
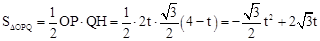 。
。∴所求△OPQ的面积S与时间t的函数关系式为:
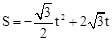 (2≤t≤3)。
(2≤t≤3)。(3)根据题意可知,0≤t≤3。
当0≤t≤2时,点Q在BC边上运动,此时,OP=2t,
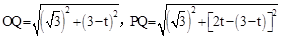 。
。∵OD=1,CD=
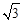 ,∴
,∴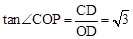 。∴
。∴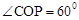 。
。∵
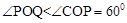 ,∴若△OPQ为直角三角形,只能是
,∴若△OPQ为直角三角形,只能是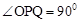 或
或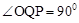 。
。若
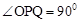 ,则
,则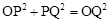 ,即
,即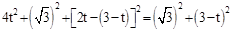 ,
,解得,
 或
或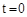 (舍去)。
(舍去)。若
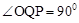 ,则
,则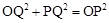 ,即
,即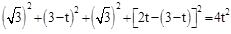 ,
,解得,
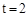 。
。当2<t≤3时,点Q在CO边上运动,此时,OP=2t>4,
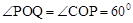 ,OQ<OC=2,
,OQ<OC=2,∴此时,△OPQ不可能为直角三角形。
综上所述,当
 或
或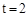 时,△OPQ为直角三角形。
时,△OPQ为直角三角形。(4)由(1)可得
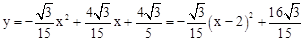 ,其对称轴为
,其对称轴为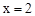 。
。又直线OB的解析式为
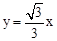 ,
,∴抛物线对称轴与OB的交点为M(0,
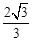 )。
)。又P(2t,0),
设过点P、M的直线解析式为
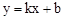 ,则
,则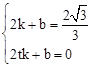 ,解得
,解得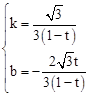 。
。∴过点P、M的直线解析式为
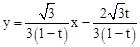 。
。又当0≤t≤2时,Q
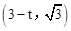 ,
,把
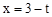 代入
代入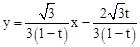 得
得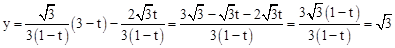 ,
,∴点Q在直线PM上,即当0≤t≤2时,点P、M、Q总在一直线上。
当2<t≤3时,
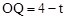 ,
,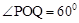 ,∴Q
,∴Q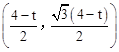 。
。代入
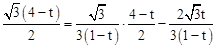 ,解得
,解得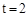 或
或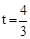 ,均不合题意,舍去。
,均不合题意,舍去。综上所述,经过A、B、C三点的抛物线的对称轴、直线OB和PQ能够交于一点,此时0≤t≤2。
(1)应用待定系数法求解即可。
(2)过点C作CD⊥x轴的于点D,过点Q作QH⊥x轴的于点H,由△OQH∽△OCD得比例式
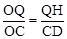 ,从而用t表示出△OPQ的边OP上的高
,从而用t表示出△OPQ的边OP上的高 ,进而根据三角形面积公式即可求得所求△OPQ的面积S与时间t的函数关系式。
,进而根据三角形面积公式即可求得所求△OPQ的面积S与时间t的函数关系式。(3)分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论。
(4)根据二次函数的性质求出抛物线对称轴
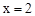 ,求出直线OB的解析式
,求出直线OB的解析式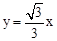 ,从而得到二者的交点
,从而得到二者的交点M(0,
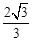 ),进而求出点P、M的直线解析式为
),进而求出点P、M的直线解析式为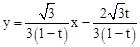 。分分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论点Q与直线
。分分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论点Q与直线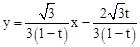 的关系,得出结论。
的关系,得出结论。
练习册系列答案
相关题目
 的图象经过点(-2,-5)、(1,4).
的图象经过点(-2,-5)、(1,4).
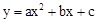 的顶点A(2,0),与y轴的交点为B(0,-1).
的顶点A(2,0),与y轴的交点为B(0,-1).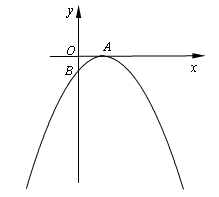
 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为
的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为 ,则
,则 ( ).
( ).
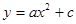 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点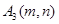 ,则
,则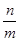 的值是 .
的值是 . 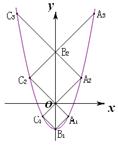

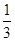 x2+bx+c经过C、D两点,求抛物线的解析式;
x2+bx+c经过C、D两点,求抛物线的解析式;
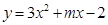 .
. 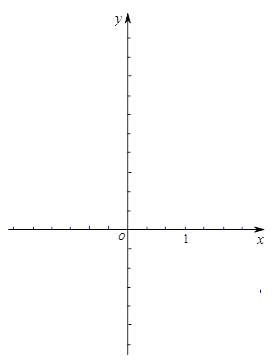
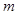 为任何实数,抛物线与x轴总有两个交点;
为任何实数,抛物线与x轴总有两个交点;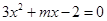 的两个有理数根都在
的两个有理数根都在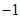 与
与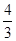 之间(不包括-1、
之间(不包括-1、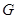 ,再将图象
,再将图象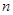 个单位,若图象
个单位,若图象