题目内容
10. 如图,点C为线段BD上一点,∠B=∠D=90°,且AC⊥CE于点C,若AB=3,DE=2,BC=6,求CD的长.
如图,点C为线段BD上一点,∠B=∠D=90°,且AC⊥CE于点C,若AB=3,DE=2,BC=6,求CD的长.
分析 根据直角三角形的性质,可得∠A+∠ACB,∠ACB+∠ECD,再根据余角的性质,可得∠A=∠ECD根据相似三角形的判定与性质,可得$\frac{AB}{CD}$=$\frac{BC}{DE}$,根据比例的性质,可得答案.
解答  解:∵在△ABC中,∠B=90°,
解:∵在△ABC中,∠B=90°,
∴∠A+∠ACB=90°.
∵AC⊥CE,
∴∠ACB+∠ECD=90°.
∴∠A=∠ECD.
∵在△ABC和△CDE中,
∠A=∠ECD,∠B=∠D=90°,
∴△ABC∽△CDE.
∴$\frac{AB}{CD}$=$\frac{BC}{DE}$.
∵AB=3,DE=2,BC=6,
∴CD=1.
点评 本题考查了相似三角形的判定与性质,利用了余角的性质,相似三角形的判定与性质,比例的性质.

练习册系列答案
相关题目
1.算式3m+n÷( )=3m-2括号中的代数式是( )
| A. | 3m+n+2 | B. | 3n-2 | C. | 3m+n+3 | D. | 3n+2 |
15.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积为( )
| A. | 4π | B. | 9π | C. | 16π | D. | 25π |
2. 如图所示,在数轴上表示|-3|的点是( )
如图所示,在数轴上表示|-3|的点是( )
 如图所示,在数轴上表示|-3|的点是( )
如图所示,在数轴上表示|-3|的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
19.下列代数式中,单项式的个数是①2x-3y;②$\frac{x}{y}$;③$\frac{x}{2}$;④-a;⑤$\frac{2}{x+1}$;⑥$\frac{1}{π}$;⑦-7x2y;⑧0( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
20.若二次根式$\sqrt{1+2x}$有意义,则x的取值范围为 ( )
| A. | x≥$\frac{1}{2}$ | B. | x≥-$\frac{1}{2}$ | C. | x≤$\frac{1}{2}$ | D. | x≤-$\frac{1}{2}$ |
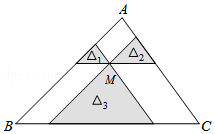 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是64.
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是64.