题目内容
【题目】如图，一次函数y＝mx+n（m≠0）的图象与反比例函数y＝
（k≠0）的图象交于第二、四象限内的点A(a，4)和点B(8，﹣1)．
（1）分别求出一次函数和反比例函数的解析式；
（2）延长AO与反比例函数交于点C，连接BC，求
ABC的面积．
【答案】（1）y＝﹣
，y＝﹣
x+3；（2）30
【解析】
（1）先把B点坐标代入
中求出得到反比例函数解析式为
，再利用反比例函数解析式把确定A（﹣2，4），然后利用待定系数法求一次函数解析式；
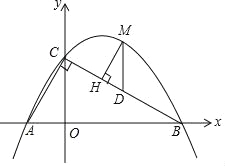
（2）先利用点A与点C关于原点对称得到C点坐标为（2，﹣4），作CD//y轴交AB于D，如图，易得D（2，2），然后根据三角形面积公式，利用S△ABC＝S△ADC+S△BDC进行计算．
解：（1）把B（8，﹣1）代入，得k＝8×（﹣1）＝﹣8，
∴反比例函数解析式为，
把A（a，4）代入得4a＝﹣8，解得a＝﹣2，
∴A（﹣2，4），
把A（﹣2，4）和B（8，﹣1）代入y＝mx+n得
，解得
∴一次函数解析式为
；
（2）∵点A与点C关于原点对称，
∴C点坐标为（2，﹣4），
作CD∥y轴交AB于D，如图，
当x＝2时，代入，解得y＝2，
∴D（2，2），
∴S△ABC＝S△ADC+S△BDC＝×（2+4）×（8+2）＝30．
故S△ABC＝30．
【题目】某医药研究所研发了一种新药，试验药效时发现：1.5小时内，血液中含药量y（微克）与时间x（小时）的关系可近似地用二次函数y＝ax2+bx表示；1.5小时后（包括1.5小时），y与x可近似地用反比例函数y＝
（k＞0）表示，部分实验数据如表：
时间x（小时） | 0.2 | 1 | 1.8 | … |
含药量y（微克） | 7.2 | 20 | 12.5 | … |
（1）求a、b及k的值；
（2）服药后几小时血液中的含药量达到最大值？最大值为多少？
（3）如果每毫升血液中含药量不少于10微克时治疗疾病有效，那么成人按规定剂量服用该药一次后能维持多长的有效时间．（
≈1.41，精确到0.1小时）
