题目内容
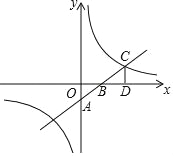
【题目】如图,直线y=﹣![]() x+
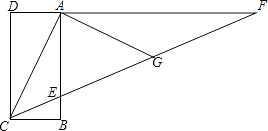
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
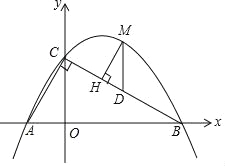
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
【答案】(1)(﹣1,0)(2)y=﹣![]() x2+
x2+![]() x+
x+![]() (3)
(3)![]()
【解析】
试题分析:(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;
(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;
(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH的周长,利用二次函数的性质可求得其最大值.
试题解析: (1)∵直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,
分别与x轴、y轴交于B、C两点,
∴B(3,0),C(0,![]() ),
),
∴OB=3,OC=![]() ,
,
∴tan∠BCO=![]() =
=![]() ,
,
∴∠BCO=60°,
∵∠ACB=90°,
∴∠ACO=30°,
∴![]() =tan30°=
=tan30°=![]() ,即
,即![]() =
=![]() ,解得AO=1,
,解得AO=1,
∴A(﹣1,0);
(2)∵抛物线y=ax2+bx+![]() 经过A,B两点,
经过A,B两点,
∴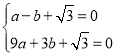 ,解得
,解得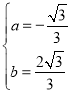 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+
x+![]() ;
;
(3)∵MD∥y轴,MH⊥BC,
∴∠MDH=∠BCO=60°,则∠DMH=30°,
∴DH=![]() DM,MH=
DM,MH=![]() DM,
DM,
∴△DMH的周长=DM+DH+MH=DM+![]() DM+
DM+![]() DM=
DM=![]() DM,
DM,
∴当DM有最大值时,其周长有最大值,
∵点M是直线BC上方抛物线上的一点,
∴可设M(t,﹣![]() t2+
t2+![]() t+
t+![]() ),则D(t,﹣
),则D(t,﹣![]() t+
t+![]() ),
),
∴DM=﹣![]() t2+
t2+![]() t+
t+![]() ),则D(t,﹣
),则D(t,﹣![]() t+
t+![]() ),
),
∴DM=﹣![]() t2+
t2+![]() t+
t+![]() ﹣(﹣
﹣(﹣![]() t+
t+![]() )=﹣
)=﹣![]() t2+
t2+![]() t=﹣
t=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,DM有最大值,最大值为
时,DM有最大值,最大值为![]() ,
,
此时![]() DM=
DM=![]() ×
×![]() =
=![]() ,
,
即△DMH周长的最大值为![]() .
.