题目内容
如图,在直角坐标平面xOy内,点A在x轴的正半轴上,点B在第一象限内,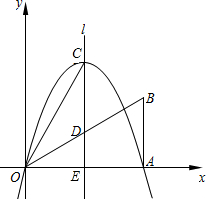 且∠OAB=90°,∠BOA=30°,OB=4.二次函数y=-x2+bx的图象经过点A,顶点为点C.
且∠OAB=90°,∠BOA=30°,OB=4.二次函数y=-x2+bx的图象经过点A,顶点为点C.(1)求这个二次函数的解析式,并写出顶点C的坐标;
(2)设这个二次函数图象的对称轴l与OB相交于点D,与x轴相交于点E,求
| DE | DC |
(3)设P是这个二次函数图象的对称轴l上一点,如果△POA的面积与△OCE的面积相等,求点P的坐标.
分析:(1)由∠OAB=90°,在直角三角形OAB中求得点A,代入函数式解得.
(2)直角三角形OAB中求得AB的长度,由抛物线的对称轴可知DE∥AB,OE=AE.求得DE,进而求得CD,从而求得.(3)利用三角形OCE和三角形POA的面积相等即求得.
(2)直角三角形OAB中求得AB的长度,由抛物线的对称轴可知DE∥AB,OE=AE.求得DE,进而求得CD,从而求得.(3)利用三角形OCE和三角形POA的面积相等即求得.
解答:解:(1)∵∠OAB=90°,∠BOA=30°,OB=4,
∴OA=OB•cos30°=2
.
∴A(2
,0).(1分)
∵二次函数y=-x2+bx的图象经过点A,
∴-(2
)2+2
b=0.
解得b=2
.
∴二次函数的解析式为y=-x2+2
x.(2分)
顶点C的坐标是(
,3).(1分)
(2)∵∠OAB=90°,∠BOA=30°,OB=4,
∴AB=2.(1分)
由DE是二次函数y=-x2+2
x的图象的对称轴,
可知DE∥AB,OE=AE.
∴
=
=
.即得DE=1.(1分)
又∵C(
,3),∴CE=3.
即得CD=2.(1分)
∴
=
.(1分)
(3)根据题意,可设P(
,n).
∵OE=
OA=
,CE=3,
∴S△OCE=
OE•CE=
.(1分)
∴S△POA=
OA•PE=
×2
|n|=
.
解得n=±
.(1分)
∴点P的坐标为P1(
,
)、P2(
,-
).(2分)
∴OA=OB•cos30°=2
| 3 |
∴A(2
| 3 |
∵二次函数y=-x2+bx的图象经过点A,
∴-(2
| 3 |
| 3 |
解得b=2
| 3 |
∴二次函数的解析式为y=-x2+2
| 3 |
顶点C的坐标是(
| 3 |
(2)∵∠OAB=90°,∠BOA=30°,OB=4,
∴AB=2.(1分)
由DE是二次函数y=-x2+2
| 3 |
可知DE∥AB,OE=AE.
∴
| DE |
| AB |
| OE |
| OA |
| 1 |
| 2 |
又∵C(
| 3 |
即得CD=2.(1分)
∴
| DE |
| DC |
| 1 |
| 2 |
(3)根据题意,可设P(
| 3 |
∵OE=
| 1 |
| 2 |
| 3 |
∴S△OCE=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
∴S△POA=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
解得n=±
| 3 |
| 2 |
∴点P的坐标为P1(
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题考查了二次函数的综合运用,考查了直角三角形内的三角函数,抛物线过一点,即代入求得;通过抛物线的对称轴来做题,方便快捷,这也考查了灵活的思维;通过面积的求得,来求得点的做标,只是考查的手段,问题考查的思路.

练习册系列答案
相关题目
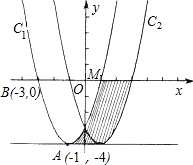 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)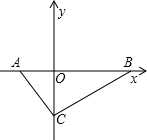 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=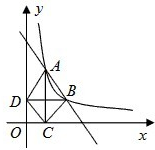 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是