Question

已知A、B是反比例函数y=

2

x

的图象上的两点，A、B的横坐标分别是3，5．设O为原点，则△AOB的面积是

16 15

.

．

Answer 1

分析：过A点作AC⊥x轴，过B点作BD⊥x轴，垂足分别为C、D，根据已知条件可求A（3，

2

3

），B（5，

2

5

），再利用S_△AOB=S_△AOC+S_梯形ACDB-S_△BOD求面积．

解答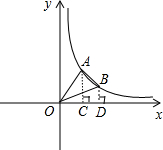：解：如图，过A点作AC⊥x轴，过B点作BD⊥x轴，垂足分别为C、D，
∵A、B两点在反比例函数y=

2

x

的图象上，且A、B的横坐标分别是3，5，
∴A（3，

2

3

），B（5，

2

5

），
∴S_△AOB=S_△AOC+S_梯形ACDB-S_△BOD
=

1

2

×3×

2

3

+

1

2

×（

2

3

+

2

5

）×（5-3）-

1

2

×5×

2

5

=

16

15

．
故本题答案为：

16

15

．

点评：本题考查了反比例函数图象上点的坐标特点．关键是将求不规则三角形的面积的问题转化为几个图形面积的和差的形式求解．