题目内容
 如图,在△ABC中,AB=3cm,BC=4cm,D是BC中点,E是AB中点,且AD⊥CE,垂足为F,求AC的长.
如图,在△ABC中,AB=3cm,BC=4cm,D是BC中点,E是AB中点,且AD⊥CE,垂足为F,求AC的长.考点:勾股定理,三角形的重心
专题:计算题
分析:连接DE,BF,延长AD作BH⊥AD于H,由D,E分别为BC,AB的中点,可得DE∥AC,AE=BE=
AB=
,BD=DC=
BC=2,再根据三角形的面积得到AF=2DF,同理可得:CF=2EF,再根据勾股定理即可得到AC的长.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答: 解:如图,连接DE,BF,延长AD作BH⊥AD于H
解:如图,连接DE,BF,延长AD作BH⊥AD于H
∵D,E分别为BC,AB的中点
∴DE∥AC,AE=BE=
AB=
,BD=DC=
BC=2
∴S△AEF=S△BEF,S△BDF=S△CDF,S△ACD=S△ACE
∴S△AEF=S△ACE-S△ACF=S△ACD-S△ACF=S△CDF
∴S△AEF=S△BEF=S△BDF=S△CDF
∴S△ABF=S△AEF+S△BEF=2S△BDF
即:
AF×BH=2×
DF×BH
∴AF=2DF
同理可得:CF=2EF
设FF=a,DF=b,则CF=2a,AF=2b
∵AD⊥CF
∴EF2+AF2=AE2;DF2+CF2=DC2,AF2+CF2=AC2
即:
(①+②)÷5得:a2+b2=
,
∴4a2+4b2=5,
即:CF2+AF2=5=AC2,
∴AC=
.
 解:如图,连接DE,BF,延长AD作BH⊥AD于H
解:如图,连接DE,BF,延长AD作BH⊥AD于H∵D,E分别为BC,AB的中点
∴DE∥AC,AE=BE=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴S△AEF=S△BEF,S△BDF=S△CDF,S△ACD=S△ACE
∴S△AEF=S△ACE-S△ACF=S△ACD-S△ACF=S△CDF
∴S△AEF=S△BEF=S△BDF=S△CDF
∴S△ABF=S△AEF+S△BEF=2S△BDF
即:
| 1 |
| 2 |
| 1 |
| 2 |
∴AF=2DF
同理可得:CF=2EF
设FF=a,DF=b,则CF=2a,AF=2b
∵AD⊥CF
∴EF2+AF2=AE2;DF2+CF2=DC2,AF2+CF2=AC2
即:
|
(①+②)÷5得:a2+b2=
| 5 |
| 4 |
∴4a2+4b2=5,
即:CF2+AF2=5=AC2,
∴AC=
| 5 |
点评:本题考查了勾股定理,三角形的面积,方程思想,主要考查了学生的推理能力,综合性比较强,有一定的难度.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
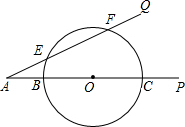 已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:
已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求: 某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%(盈利率=
某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%(盈利率=
 如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为10cm,则四边形EFGH的周长是
如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为10cm,则四边形EFGH的周长是