题目内容
如图，若以正方形ABCD的对角线AC为边作第二个正方形ACFE，再以它的对角线CE为边作第三个正方形CEGH，如此下去，设S1=S正方形ABCD=1，S2=S正方形ACFE，S3=S正方形CEGH，…，那么第八个正方形的面积S8=________，第n个正方形的面积Sn=________．
27 2n-1
分析：根据正方形的性质易得：正方形的对角线是正方形的边长的
倍；进而根据题意，找到第二个正方形与第一个正方形面积的关系，依此类推，可得第n个正方形Sn的面积．
解答：根据勾股定理得：正方形的对角线是正方形的边长的倍；
即第二个正方形的面积是第一个正方形面积的2倍，即是2，…
依此类推第n个正方形的面积是上一个正方形面积的2倍，即2×2×2…×2（n-1个2）=2n-1，
故S8=27，
故答案为27、2n-1．
点评：本题主要考查正方形的性质，要求学生能够根据勾股定理得到前后正方形的边长之间的关系，进一步得到面积之间的关系．从而找到规律．
分析：根据正方形的性质易得：正方形的对角线是正方形的边长的
倍；进而根据题意，找到第二个正方形与第一个正方形面积的关系，依此类推，可得第n个正方形Sn的面积．解答：根据勾股定理得：正方形的对角线是正方形的边长的
倍；即第二个正方形的面积是第一个正方形面积的2倍，即是2，…
依此类推第n个正方形的面积是上一个正方形面积的2倍，即2×2×2…×2（n-1个2）=2n-1，
故S8=27，
故答案为27、2n-1．
点评：本题主要考查正方形的性质，要求学生能够根据勾股定理得到前后正方形的边长之间的关系，进一步得到面积之间的关系．从而找到规律．
练习册系列答案
相关题目
如图，分别以正方形ABCD的边AB、BC为直径画半圆，若正方形的边长为a，则阴影部分面积
如图，分别以正方形ABCD的边AB、BC为直径画半圆，若正方形的边长为a，则阴影部分面积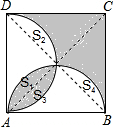
小华在某课外书上看到了这样一道题：“如图，分别以正方形ABCD的边AB、AD为直径画半圆．若正方形的边长为a，求阴影部分的面积．”从表面上看，图中的阴影部分是复杂且比较分散的图形，要直接计算它的面积还是有困难的，但小华仔细考虑过后，只是将正方形的对角线AC、BD连接起来，然后利用自己所学的“图形的旋转”知识很简便地就将本题解决了，你知道他是怎样做的吗？
