题目内容
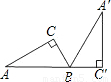
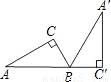
 如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.
如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.
解:∵∠C=90°,BC=2,AB=4,
∴∠A=30°.
∴∠ABC=60°.
根据旋转的性质,得∠A′BC′=∠ABC=60°.
则∠ABA′=120°.
∴S= =
= =
= .
.
故斜边AB旋转到A′B所扫过的扇形面积为 .
.
分析:根据直角三角形的性质可知∠A=30°,∠ABC=60°,根据旋转的性质得∠A′BC′=60°,则∠ABA′=120°,从而根据扇形面积公式S= 进行计算.
进行计算.
点评:本题考查扇形面积的计算,要求掌握扇形的面积公式:(1)利用圆心角和半径:S= ;(2)利用弧长和半径:S=
;(2)利用弧长和半径:S= lr,学会针对不同的题型选择合适的方法.
lr,学会针对不同的题型选择合适的方法.
∴∠A=30°.
∴∠ABC=60°.
根据旋转的性质,得∠A′BC′=∠ABC=60°.
则∠ABA′=120°.
∴S=
 =
= =
= .
.故斜边AB旋转到A′B所扫过的扇形面积为
 .
.分析:根据直角三角形的性质可知∠A=30°,∠ABC=60°,根据旋转的性质得∠A′BC′=60°,则∠ABA′=120°,从而根据扇形面积公式S=
 进行计算.
进行计算.点评:本题考查扇形面积的计算,要求掌握扇形的面积公式:(1)利用圆心角和半径:S=
 ;(2)利用弧长和半径:S=
;(2)利用弧长和半径:S= lr,学会针对不同的题型选择合适的方法.
lr,学会针对不同的题型选择合适的方法. 
练习册系列答案
相关题目
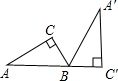 如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则斜边AB旋转到A′B所扫过的扇形面积为( )
如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则斜边AB旋转到A′B所扫过的扇形面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A、B、C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则斜边AB旋转到A′B所扫过的扇形面积为
如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A、B、C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则斜边AB旋转到A′B所扫过的扇形面积为 如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则斜边AB旋转到A′B所扫过的扇形面积为
如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则斜边AB旋转到A′B所扫过的扇形面积为