题目内容
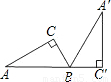
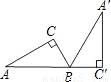
如图，Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得，且点A，B，C′在同一条直线上，在Rt△ABC中，若∠C=90°，BC=2，AB=4，则斜边AB旋转到A′B所扫过的扇形面积为| 16π |
| 3 |
| 16π |
| 3 |
| 8π |
| 3 |
| 8π |
| 3 |
分析：根据直角三角形的性质，得∠A=30°，根据直角三角形的两个锐角互余，得∠ABC=60°，根据旋转的性质得∠A′BC′=60°，则∠ABA′=120°，从而根据扇形面积公式计算即可；利用弧长公式即可求出A在旋转过程中走过的路线长．
解答：解：∵∠C=90°，BC=2，AB=4，
∴∠A=30°．
∴∠ABC=60°．
根据旋转的性质，得∠A′BC′=∠ABC=60°．
则∠ABA′=120°．
所以S=
=
，
∴点A在旋转过程中走过的路线长l=
=
，
故答案为：
，
．
∴∠A=30°．
∴∠ABC=60°．
根据旋转的性质，得∠A′BC′=∠ABC=60°．
则∠ABA′=120°．
所以S=
| nπr2 |
| 360 |
| 16π |
| 3 |
∴点A在旋转过程中走过的路线长l=
| nπr |
| 180 |
| 8π |
| 3 |
故答案为：
| 16π |
| 3 |
| 8π |
| 3 |
点评：此题综合运用了直角三角形的性质，即30°所对的直角边是斜边的一半；旋转的性质，即旋转前后的图形全等，则对应角相等；扇形的面积公式和弧长公式．
练习册系列答案
相关题目
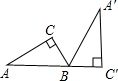如图，Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得，且点A，B，C′在同一条直线上，在Rt△ABC中，若∠C=90°，BC=2，AB=4，则斜边AB旋转到A′B所扫过的扇形面积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得，且点A、B、C′在同一条直线上，在Rt△ABC中，若∠C=90°，BC=2，AB=4，则斜边AB旋转到A′B所扫过的扇形面积为
