题目内容
正方形 、正方形
、正方形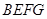 和正方形
和正方形 的位置如图所示,点
的位置如图所示,点 在线段
在线段 上,正方形
上,正方形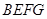 的边长为4,则
的边长为4,则 的面积为:( )
的面积为:( )

 、正方形
、正方形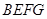 和正方形
和正方形 的位置如图所示,点
的位置如图所示,点 在线段
在线段 上,正方形
上,正方形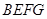 的边长为4,则
的边长为4,则 的面积为:( )
的面积为:( )
| A.10 | B.12 | C.14 | D.16 |
D
解答:解:设AB=a,FP=b,延长PK,BE交于点M,

∵四边形ABCD为正方形,
∴AB=AD=CD=BC=a,
∴S△AED= (4+a)a,
(4+a)a,
∵CG=BC-BG=a-4,
∴S△CGD= (a-4)a,
(a-4)a,
∵四边形FPRK为正方形,
∴FR=RK=PK=FP=b,
∵GF=4,
∴S△KPG= (4+b)b,
(4+b)b,
∵四边形FEBG、FPKR为正方形,
∴∠MBG=∠BGP=∠P=90°,
∴矩形FPME,
∴PM="4" KM=4-b,
∵EM=b,
∴S△EKM= (4-b)b,
(4-b)b,
∴S△DKE=(S正方形ABCD+S正方形GFEB+S矩形FPME)-(S△AED+S△CGD+S△GPK+S△EMK),
=(a2+42+4b)-[ (4+a)a+
(4+a)a+ (a-4)a+
(a-4)a+ (4+b)b+
(4+b)b+ (4-b)b],
(4-b)b],
=a2+16+4b-[2a+ a2+
a2+ a2-2a+2b+
a2-2a+2b+ b2+2b-
b2+2b- b2]
b2]
=a2+16+4b-[a2+4b]
=16;

∵四边形ABCD为正方形,
∴AB=AD=CD=BC=a,
∴S△AED=
 (4+a)a,
(4+a)a,∵CG=BC-BG=a-4,
∴S△CGD=
 (a-4)a,
(a-4)a,∵四边形FPRK为正方形,
∴FR=RK=PK=FP=b,
∵GF=4,
∴S△KPG=
 (4+b)b,
(4+b)b,∵四边形FEBG、FPKR为正方形,
∴∠MBG=∠BGP=∠P=90°,
∴矩形FPME,
∴PM="4" KM=4-b,
∵EM=b,
∴S△EKM=
 (4-b)b,
(4-b)b,∴S△DKE=(S正方形ABCD+S正方形GFEB+S矩形FPME)-(S△AED+S△CGD+S△GPK+S△EMK),
=(a2+42+4b)-[
 (4+a)a+
(4+a)a+ (a-4)a+
(a-4)a+ (4+b)b+
(4+b)b+ (4-b)b],
(4-b)b],=a2+16+4b-[2a+
 a2+
a2+ a2-2a+2b+
a2-2a+2b+ b2+2b-
b2+2b- b2]
b2]=a2+16+4b-[a2+4b]
=16;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的点,且△ACE是等边三角形.
上的点,且△ACE是等边三角形.

 的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C之间的距离).若AB=40cm,当
的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C之间的距离).若AB=40cm,当 变为
变为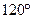 时,千斤顶升高了多少?
时,千斤顶升高了多少?
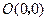 ,
,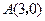 ,
,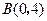 ,请你画出
,请你画出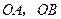 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形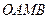 ;
;
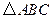 绕顶点
绕顶点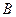 按顺时针方向旋转
按顺时针方向旋转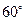 ,得到
,得到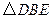 ,连结
,连结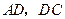 ,
,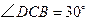 .求证:
.求证: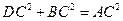 ,即四边形
,即四边形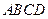 是勾股四边形
是勾股四边形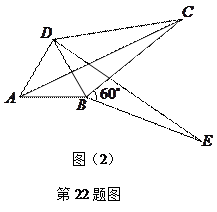

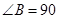 °。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。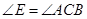
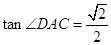 ,求BC的长。(8分)
,求BC的长。(8分) 、
、 上,
上, ^
^ ^
^ 、
、
 =
=
 =
=