题目内容
 如图所示是一块空地,AD=
如图所示是一块空地,AD=| 5 |
分析:连接AC,在直角三角形ADC中,由AD及CD的长,利用勾股定理求出AC的长,再由AC,BC及AB的长,利用勾股定理的逆定理得到三角形ABC为直角三角形,空地的面积=直角三角形ABC的面积-直角三角形ADC的面积,求出即可.
解答: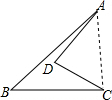 解:连接AC,
解:连接AC,
∵∠ADC=90°,
∴△ADC为直角三角形,又AD=
cm,CD=2cm,
∴AC2=AD2+CD2=(
)2+22=9,即AC=3cm,
又BC=4cm,AB=5cm,
∴AC2+BC2=9+42=25,AB2=52=25,
∴AC2+BC2=AB2,
∴∠ACB=90°,即△ABC为直角三角形,
∴S空地=S△ABC-S△ADC=
AC•BC-
DC•AD=
×3×4-
×2×
=6-
(cm2)
 解:连接AC,
解:连接AC,∵∠ADC=90°,
∴△ADC为直角三角形,又AD=
| 5 |
∴AC2=AD2+CD2=(
| 5 |
又BC=4cm,AB=5cm,
∴AC2+BC2=9+42=25,AB2=52=25,
∴AC2+BC2=AB2,
∴∠ACB=90°,即△ABC为直角三角形,
∴S空地=S△ABC-S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
点评:此题考查了勾股定理,以及勾股定理的逆定理,熟练掌握勾股定理及逆定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
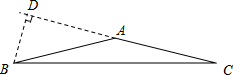 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?
某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?
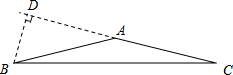 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?
某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?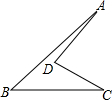 如图所示是一块空地,AD=
如图所示是一块空地,AD= cm,CD=2cm,AB=5cm,BC=4cm,∠ADC=90°.求这块空地的面积.
cm,CD=2cm,AB=5cm,BC=4cm,∠ADC=90°.求这块空地的面积.