题目内容
 如图,直角△ABC中∠C=90°,∠A=30°,BC=2,则△ABC的内切圆⊙O1的半径r1=
如图,直角△ABC中∠C=90°,∠A=30°,BC=2,则△ABC的内切圆⊙O1的半径r1=考点:三角形的内切圆与内心
专题:规律型
分析:本题可将三角形ABO分解成三个三角形,再根据三个三角形的面积之和等于△ABO的面积,即可得出半径的值,再根据题意依次列出⊙O2,⊙O3…的半径大小,找出规律即可.
解答:解:(1)∵BC=2,∠C=90°,∠A=30°,
∴B(0,2),A(2
,0),
则SOO1B=
×OB×r1=r1,
SAO1O=
×AO×r1=
r1
SAO1B=
×AB×r1=2r1
SAOB=
×2×2
=2
;
∵SAOB=SOO1B+SAO1O+SAO1B=(3+
)r1=2
,
∴r1=
-1;
(2)根据题意得:R1=
-1,R2=
,R3=
…
∴Rn=
,
依此类推可得:R2014=
,
故答案为:
-1,
.
∴B(0,2),A(2
| 3 |
则SOO1B=
| 1 |
| 2 |
SAO1O=
| 1 |
| 2 |
| 3 |
SAO1B=
| 1 |
| 2 |
SAOB=
| 1 |
| 2 |
| 3 |
| 3 |
∵SAOB=SOO1B+SAO1O+SAO1B=(3+
| 3 |
| 3 |
∴r1=
| 3 |
(2)根据题意得:R1=
| 3 |
| ||
| 3 |
| ||
| 32 |
∴Rn=
| ||
| 3n-1 |
依此类推可得:R2014=
| ||
| 32013 |
故答案为:
| 3 |
| ||
| 32013 |
点评:本题考查的是三角形的性质,解此类题目时要根据题意列出不等式,适当地对图形进行分解,然后再解题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
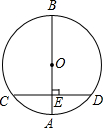 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段AE的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段AE的长为( )| A、4 | B、3 | C、2 | D、6 |
 已知:如图,在Rt△ABC中,∠C=90°,AB=10,sinA=
已知:如图,在Rt△ABC中,∠C=90°,AB=10,sinA= 如图,图形中的折线是迷宫路线,沿着其中的路线才能由A顺利到达B点,从而走出迷宫,迷宫中的AB距离
如图,图形中的折线是迷宫路线,沿着其中的路线才能由A顺利到达B点,从而走出迷宫,迷宫中的AB距离