题目内容
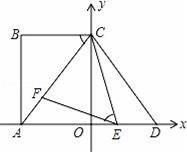
如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.


【考点】平行线的判定与性质.
【分析】∠C与∠AED相等,理由为:由邻补角定义得到∠1与∠DFE互补,再由已知∠1与∠2互补,根据同角的补角相等可得出∠2与∠DFE相等,根据内错角相等两直线平行,得到AB与EF平行,再根据两直线平行内错角相等可得出∠3与∠ADE相等,由已知∠B与∠3相等,利用等量代换可得出∠B与∠ADE相等,根据同位角相等两直线平行得到DE与BC平行,再根据两直线平行同位角相等可得证.
【解答】解:∠C与∠AED相等,理由为:
证明:∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义),
∴∠2=∠DFE(同角的补角相等),
∴AB∥EF(内错角相等两直线平行),
∴∠3=∠ADE(两直线平行内错角相等),
又∠B=∠3(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等两直线平行),
∴∠C=∠AED(两直线平行同位角相等).

练习册系列答案
相关题目



 cm,弦BD的长为3cm,求CF的长.
cm,弦BD的长为3cm,求CF的长.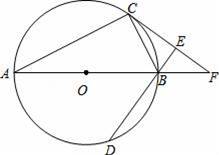



 的结果等于( )
的结果等于( )




 ,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.