题目内容

已知正六边形ABCDEF内接于⊙O，图中阴影部分的面积为12 $数学公式$ ，则⊙O的半径为

A.
3
B.
4
C.
5
D.
6

B
分析：要求三角形的面积就要先求出它的边长，根据正多边形与圆的关系即可求出．
解答：

解：连接DO并延长，交BF于点G．
∵正六边形ABCDEF内接于⊙O，
∴阴影部分为正三角形，
设边长是a，则
FG= $\text{[math]}$ a，DG= $\text{[math]}$ a，
则面积是 $\text{[math]}$ a× $\text{[math]}$ a= $\text{[math]}$ ，
得到 $\text{[math]}$ =12 $\text{[math]}$ ，
解得a=4 $\text{[math]}$ ，
则DG=BD•sin60°=4 $\text{[math]}$ × $\text{[math]}$ =6
因而半径OD= $\text{[math]}$ DG=6× $\text{[math]}$ =4．
故选：B．
点评：本题主要考查了正多边形的计算，得出阴影部分三角形的边长是解题关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

（1）已知：如图1，△ABC是⊙O的内接正三角形，点P为

上一动点，求证：PA=PB+PC．
下面给出一种证明方法，你可以按这一方法补全证明过程，也可以选择另外的证明方法．
证明：在AP上截取AE=CP，连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
（2）如图2，四边形ABCD是⊙O的内接正方形，点P为

上一动点，求证：PA=PC+

PB．
（3）如图3，六边形ABCDEF是⊙O的内接正六边形，点P为

上一动点，请探究PA、PB、PC三者之间有何数量关系，直接写出结论．

（1）已知：如图1，△ABC为正三角形，点M、N分别在BC、CA边上，且BM=CN，BN与AM相交于Q点，试求∠BQM的度数．
解：∵△ABC为正三角形，∴∠ABC=∠ACB=60°，AB=BC．
在△ABM和△BCN中，

?△ABM≌△BCN（

，
∴∠BQM=∠

°．
（2）如果将（1）中的正三角形改为正方形ABCD（如图2），点M、N分别在BC、CD边上，且BM=CN，BN与AM相交于Q点，那么∠BQM等于多少度呢？说明理由．

（3）如果将（1）中的“正三角形”改为正五边形、正六边形、…、正n边形（如图3），其余条件都不变，请你根据（1）（2）的求解思路，将你推断的结论填入下表：（正多边形的各个内角都相等）

正多边形	正五边形	正六边形	…	正n边形
∠BQM的度数			…

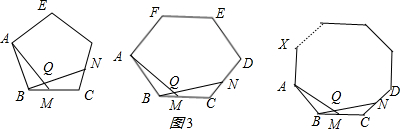
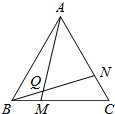（1）已知△ABC为正三角形，点M是BC上一点，点N是AC上一点，AM、BN相交于点Q，∠BAM=∠NBC，猜想∠BQM等于多少度，并证明你的猜想．
（2）将（1）中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、正六边形ABCDEF、正n边形ABCD…X，“点N是AC上一点”改为点N是CD上一点，其余条件不变，分别推断出∠BQM等于多少度，将结论填入下表：

正多边形	正方形	正五边形	正六边形	…	正n边形
∠BQM的度数				…

（2012•石家庄二模）阅读下列材料：
问题：如图1，在正方形ABCD内有一点P，PA=

，PC=1，求∠BPC的度数．
小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连接PP′．
请你参考小明同学的思路，解决下列问题：
（1）图2中∠BPC的度数为

；
（2）如图3，若在正六边形ABCDEF内有一点P，且PA=2

，PB=4，PC=2，则∠BPC的度数为

，正六边形ABCDEF的边长为

如图1，在正方形ABCD内有一点P，PA=

，PC=1，求∠BPC的度数．
【分析问题】根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．
【解决问题】请你通过计算求出图2中∠BPC的度数；
【比类问题】如图3，若在正六边形ABCDEF内有一点P，且PA=2

，PB=4，PC=2．
（1）∠BPC的度数为

；
（2）直接写出正六边形ABCDEF的边长为