题目内容
设a，b，c分别是△ABC的三边长，且
=
，则它的内角∠A、∠B的关系是（ ）
| a |
| b |
| a+b |
| a+b+c |
| A、∠B＞2∠A |
| B、∠B=2∠A |
| C、∠B＜2∠A |
| D、不确定 |
分析：根据
=
即可求得
=
，延长CB至D，使BD=AB，即可求证△ABC∽△DAC，即可得∠ABC=∠D+∠BAD=2∠D=2∠BAC．即可解题．
| a |
| b |
| a+b |
| a+b+c |
| a |
| b |
| b |
| a+c |
解答：
解：由
=
得
=
，
延长CB至D，使BD=AB，
于是CD=a+c，
在△ABC与△DAC中，∠C为公共角，
且BC：AC=AC：DC，
∴△ABC∽△DAC，∠BAC=∠D，
∵∠BAD=∠D，
∴∠ABC=∠D+∠BAD=2∠D=2∠BAC．
故选B．
解：由| a |
| b |
| a+b |
| a+b+c |
| a |
| b |
| b |
| a+c |
延长CB至D，使BD=AB，
于是CD=a+c，
在△ABC与△DAC中，∠C为公共角，
且BC：AC=AC：DC，
∴△ABC∽△DAC，∠BAC=∠D，
∵∠BAD=∠D，
∴∠ABC=∠D+∠BAD=2∠D=2∠BAC．
故选B．
点评：本题考查了相似三角形对应边比值相等的性质，相似三角形的判定，本题中求证△ABC∽△DAC是解题的关键．
练习册系列答案
相关题目
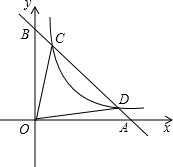于A、B两点，设C、D的坐标分别是（x1，y1）、（x2，y2），连接OC、OD．
如图，过反比例函数y=
如图所示的长方形中，甲、乙、丙、丁四块面积相等，甲的长是宽的2倍，设乙的长和宽分别是a和b，则a：b=